
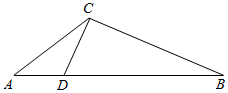
 如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,
如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,分析 (I)分别在△ACD和△BCD中使用正弦定理,根据sin∠ADC=sin∠BDC和$\frac{AD}{DB}=\frac{1}{3}$得出结论.
(II)利用(I)的结论可知$\frac{AC}{BC}=\frac{2}{3}$,在△ABC中使用余弦定理解出BC.
解答 解:(Ⅰ)在△ACD中,由正弦定理得:$\frac{AC}{sin∠ADC}=\frac{AD}{sinα}$,
在△BCD中,由正弦定理得:$\frac{BC}{sin∠BDC}=\frac{BD}{sinβ}$,
∵∠ADC+∠BDC=π,∴sin∠ADC=sin∠BDC,
∵$\frac{AD}{DB}=\frac{1}{3}$,∴$\frac{AC}{BC}=\frac{sinβ}{3sinα}$.
(Ⅱ)∵$α=\frac{π}{6}$,$β=\frac{π}{2}$,
∴$\frac{AC}{BC}=\frac{sinβ}{3sinα}=\frac{2}{3}$,∠ACB=α+β=$\frac{2π}{3}$.
设AC=2k,BC=3k,k>0,由余弦定理得:AB2=AC2+BC2-2AC•BC•cos∠ACB,
即$19=4{k^2}+9{k^2}-2•2k•3k•cos\frac{2π}{3}$,
解得k=1,∴BC=3.
点评 本题考查了正弦定理,余弦定理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-$\frac{9}{5}$) | B. | (-$\frac{9}{5}$,11) | C. | (-$\frac{9}{5}$,-1) | D. | (-5,11) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
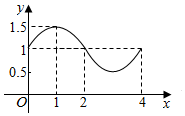 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )| A. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016 | B. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016$\frac{1}{2}$ | ||
| C. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017$\frac{1}{2}$ | D. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q是真命题 | B. | p∧(﹁q)是真命题 | C. | ﹁p∧q是真命题 | D. | ﹁p∧﹁q是假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com