
分析 (1)由y=x2-8,令y=0,解得x,可得c,利用a2-b2=c2,及其得$4×\frac{1}{2}$ab=6,解出即可得出.
(2)不妨设直线AB的方程x=ky+m,设A(x1,y1),B(x2,y2).与椭圆方程联立可得(k2+9)y2+2kmy+m2-9=0,由AD⊥BD,可得$\overrightarrow{DA}•\overrightarrow{DB}$=0,利用根与系数的关系、数量积运算性质可得m.利用S△ABD=$\frac{1}{2}|DE|$|y1-y2|,即为二次函数的单调性即可得出.
解答 解:(1)由y=x2-8,令y=0,得x=±2$\sqrt{2}$,则c=2$\sqrt{2}$,
∴a2-b2=8 ①.
又由题意,得$4×\frac{1}{2}$ab=6,即ab=3 ②.
由①②解得a=3,b=1,
故椭圆C的方程为:$\frac{{x}^{2}}{9}$+y2=1.
(2)不妨设直线AB的方程x=ky+m,设A(x1,y1),B(x2,y2).
由$\left\{\begin{array}{l}{x=ky+m}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,消去x得(k2+9)y2+2kmy+m2-9=0,
则y1+y2=$\frac{-2km}{{k}^{2}+9}$,y1y2=$\frac{{m}^{2}-9}{{k}^{2}+9}$.
∵AD⊥BD,
∴$\overrightarrow{DA}•\overrightarrow{DB}$=0,.
$\overrightarrow{DA}$=(x1-3,y1),$\overrightarrow{DB}$=(x2-3,y2),得(x1-3)(x2-3)+y1y2=0.
∴(k2+1)y1y2+k(m-3)(y1+y2)+(m-3)2=0,
将 ①代入上式,解得m=$\frac{12}{5}$或m=3(舍).
∴$m=\frac{12}{5}$(此时直线AB经过定点E$(\frac{12}{5},0)$,与椭圆有两个交点).
∴S△ABD=$\frac{1}{2}|DE|$|y1-y2|=$\frac{1}{2}×\frac{3}{5}×$$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{9}{5}$$\sqrt{\frac{25({k}^{2}+9)-144}{25({k}^{2}+9)^{2}}}$.
设t=$\frac{1}{{k}^{2}+9}$,$0<t≤\frac{1}{9}$,则
S△ABD=$\frac{9}{5}$$\sqrt{-\frac{144}{25}{t}^{2}+t}$,
∴当t=$\frac{25}{288}$∈$(0,\frac{1}{9}]$时,S△ABD取得最大值$\frac{3}{8}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、三角形面积计算公式、斜率垂直与数量积的运算性质、二次函数的单调性,考查了推理能力与计算能力,属于难题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
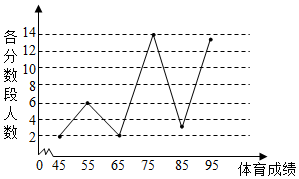 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
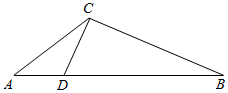 如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,
如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com