
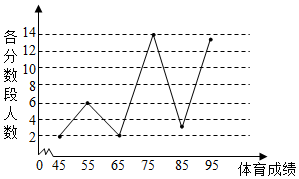
 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).分析 (Ⅰ)由折线图,知样本中体育成绩大于或等于70分的学生有30人,由此能求出该校高一年级学生中,“体育良好”的学生人数.
(Ⅱ)从这两组数据中随机抽取两个,求出所有的可能结果,在抽取的2名学生中,至少有1人体育成绩在[60,70)内的对立事件是两人的体育成绩都在[80,90)内,由此能求出至少有1人体育成绩在[60,70)的概率.
(Ⅲ)由已知能写出当数据a,b,c的方差s2最小时,a,b,c的值.
解答 解:(Ⅰ)由折线图,知样本中体育成绩大于或等于70分的学生有30人,
∴该校高一年级学生中,“体育良好”的学生人数大约有1000×$\frac{30}{40}$=750人.
(Ⅱ)设“至少有1人的体育成绩在[60,70)”为事件M,
记体育成绩在[60,70)的数据为A1,A2,体育成绩在[80,90)的数据为B1,B2,B3,
从这两组数据中随机抽取两个,所有的可能结果有:${C}_{5}^{2}=10$种,
事件M的对立事件是两人的体育成绩都在[80,90)内,
∴至少有1人体育成绩在[60,70)的概率P(M)=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$.
(Ⅲ)∵甲、乙、丙三人的体育成绩分别为a,b,c,且分别在[70,80),[80,90),[90,100]三组中,其中a,b,c∈N,
当数据a,b,c的方差s2最小时,a,b,c的值分别为70,80,100.
点评 本题考查折线图的应用,考查概率的求法,是中档题,解题时要认真审,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e=-1 | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期” | |
| B. | “m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充分不必要条件 | |
| C. | “若a≤b,则2a≤2b-1”的否命题 | |
| D. | “任意a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com