
分析 (Ⅰ)由椭圆的焦点F1,F2,过右焦点F2的直线l与C相交于P、Q两点,△PQF1的周长为短轴长的2$\sqrt{3}$倍,得到$a=\sqrt{3}b$,由此能求出椭圆C的离心率.
(Ⅱ)设椭圆方程为${x^2}+3{y^2}=\frac{3}{2}{c^2}$,直线的方程为y=x-c,代入椭圆方程得$4{x^2}-6cx+\frac{3}{2}{c^2}=0$,由此利用韦达定理、椭圆性质、向量知识,结合已知条件能求出不存在点M,使$\overrightarrow{OM}=2\overrightarrow{OP}+\overrightarrow{OQ}$成立.
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点F1,F2,过右焦点F2的直线l与C相交于P、Q两点,
△PQF1的周长为短轴长的2$\sqrt{3}$倍,△PQF1的周长为4a…(2分)
∴依题意知$4a=4\sqrt{3}b$,即$a=\sqrt{3}b$…(3分)
∴C的离心率$e=\sqrt{1-{{(\frac{b}{a})}^2}}=\frac{{\sqrt{6}}}{3}$…(4分)
(Ⅱ)设椭圆方程为${x^2}+3{y^2}=\frac{3}{2}{c^2}$,直线的方程为y=x-c,
代入椭圆方程得$4{x^2}-6cx+\frac{3}{2}{c^2}=0$…(5分)
设P(x1,y1),Q(x2,y2),则${x_1}+{x_2}=\frac{3}{2}c$,${x_1}{x_2}=\frac{3}{8}{c^2}$…(6分)
设M(x0,y0),则$x_0^2+3y_0^2=\frac{3}{2}{c^2}$①…(7分)
由$\overrightarrow{OM}=2\overrightarrow{OP}+\overrightarrow{OQ}$得$\left\{\begin{array}{l}{x_0}=2{x_1}+{x_2}\\{y_0}=2{y_1}+{y_2}\end{array}\right.$…(8分)
代入①得$4(x_1^2+3y_1^2)+x_2^2+3y_2^2+4({x_1}{x_2}+3{y_1}{y_2})=\frac{3}{2}{c^2}$…(9分)
因为$x_1^2+3y_1^2=\frac{3}{2}{c^2}$,$x_2^2+3y_2^2=\frac{3}{2}{c^2}$,
所以$\frac{3}{2}{c^2}+({x_1}{x_2}+3{y_1}{y_2})=0$②…(10分)
而${x_1}{x_2}+3{y_1}{y_2}={x_1}{x_2}+3({x_1}-c)({x_2}-c)=4{x_1}{x_2}-3c({x_1}+{x_2})+3{c^2}=0$…(11分)
从而②式不成立.
故不存在点M,使$\overrightarrow{OM}=2\overrightarrow{OP}+\overrightarrow{OQ}$成立…(12分)
点评 本题考查椭圆的离心率的求法,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意韦达定理、椭圆性质、向量知识的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | -$\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF2|=$\frac{5}{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF2|=$\frac{5}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
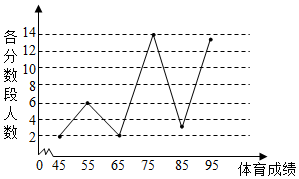 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com