
| A. | “π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期” | |
| B. | “m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充分不必要条件 | |
| C. | “若a≤b,则2a≤2b-1”的否命题 | |
| D. | “任意a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
分析 A.根据复合命题的真假关系进行判断.
B.根据函数单调性以及充分条件和必要条件的定义进行判断.
C.求出命题的否命题,根据指数函数的单调性进行判断.
D.根据含有量词的命题的否定进行判断.
解答 解:A.π是函数y=sinx的一个周期是假命题,2π是函数y=cosx的一个周期是真命题,则“π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”是真命题.
B.当x≥1时,log2x≥0,则f(x)≥m,若函数f(x)=m+log2x(x≥1)不存在零点,
则m>0,则“m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充要条件,故B是假命题,
C.“若a≤b,则2a≤2b-1”的否命题是,“若a>b,则2a>2b-1”为真命题.
∵a>b,∴2a>2b>2b-1,故C是真命题.
D.“任意a∈(0,+∞),函数y=ax在定义域内单调递增”是假命题,则“任意a∈(0,+∞),函数y=ax在定义域内单调递增”的否定是真命题,
故选:B
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件的判断,复合命题之间的关系以及四种命题的真假判断,综合性较强,但难度不大.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
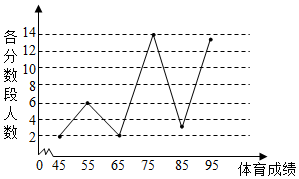 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.
环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com