
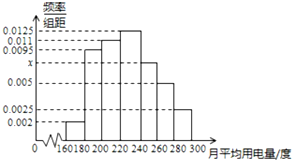
 如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.
如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.分析 (1)由频率分布直方图物性质能求出x并推导出中位数应在[220,240)内,设中位数为a,由频率分布直方图的性质列出方程,给求出月均用电量的中位数.
(2)分别求出求出月均用电量在[220,240)内的户数、在[240,260)内的户数在[260,280)内的户数、在[280,300]内的户数,求出抽取比例,从而得到X服从超几何分布,X可能取的值为0,1,2.分别求出相应的概率,由此能求出随机变量X的分布列和均值.
解答 解:(1)由(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,
解得x=0.0075; (2分)
因为(0.002+0.0095+0.011)×20=0.45<0.5,
所以中位数应在[220,240)内,
设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5,
解得a=224.(4分)
(2)月均用电量在[220,240)内的户数为0.0125×20×100=25,
在[240,260)内的户数为0.0075×20×100=15,
在[260,280)内的户数为0.005×20×100=10,
在[280,300]内的户数为0.0025×20×100=5,
从中抽取11户,抽取比例为$\frac{11}{25+15+10+5}$=$\frac{1}{5}$,
所以月均用电量在[220,240)内应抽取的户数为$25×\frac{1}{5}=5$.(7分)
用X表示这2户居民中用电量在[220,240)内的户数,
所以X服从超几何分布,X可能取的值为0,1,2.
相应的概率为$P(X=k)=\frac{{C_5^kC_6^{2-k}}}{{C_{11}^2}}(k=0,1,2)$,(9分)
分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{3}{11}$ | $\frac{6}{11}$ | $\frac{2}{11}$ |
点评 本题考查频率分布列方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意超几何分布的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{128}$ | B. | $\frac{1}{512}$ | C. | $\frac{1}{256}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x-y-7=0 | D. | x+y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com