
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真命题,真命题 | B. | 真命题,假命题 | C. | 假命题,真命题 | D. | 假命题,假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [-3,+∞) | C. | (-∞,5] | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
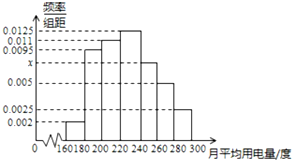 如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.
如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
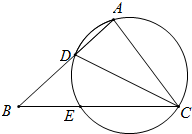 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com