
【题目】某商店经营的某种消费品的进价为每件14元,月销售量![]() (百件)与每件的销售价格
(百件)与每件的销售价格![]() (元)的关系如图所示,每月各种开支2 000元.
(元)的关系如图所示,每月各种开支2 000元.

(1)写出月销售量![]() (百件)关于每件的销售价格
(百件)关于每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(2)写出月利润![]() (元)与每件的销售价格
(元)与每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(3)当该消费品每件的销售价格为多少元时,月利润最大?并求出最大月利润.
【答案】(1) 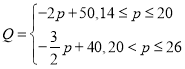 ;(2)
;(2) 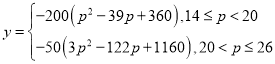 ;(3) 当该消费品每件的销售价格为学
;(3) 当该消费品每件的销售价格为学![]() 时,月利润最大,为4050元
时,月利润最大,为4050元
【解析】
(1)根据函数的图象为分段函数,分别求得当![]() 和
和![]() 时,求得函数的解析式,即可得到答案;
时,求得函数的解析式,即可得到答案;
(2)由(1)中的函数,结合题意,即可求得月利润![]() (元)与每件的销售价格
(元)与每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(3)由(2)中的解析式,结合二次函数的性质,分别求得当![]() 和
和![]() 的最大值,即可求解.
的最大值,即可求解.
(1)由题意,当![]() 时,设函数
时,设函数![]() ,
,
由![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
同理可得当![]() 时,
时,![]() ,
,
所以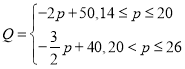 .
.
(2)当![]() 时,
时,![]() ,
,
即![]() ;
;
当![]() 时,
时,![]() ,
,
即![]() ,
,
所以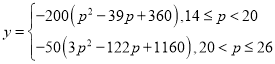 .
.
(3)由(2)中的解析式和二次函数的知识,可得
当![]() 时,则
时,则![]() 时,
时,![]() 取到最大值,为4050;
取到最大值,为4050;
当![]() 时,则
时,则![]() 时,
时,![]() 取到最大值,为
取到最大值,为![]() .
.
又由![]() ,所以当该消费品每件的销售价格为学
,所以当该消费品每件的销售价格为学![]() 时,月利润最大,为4050元.
时,月利润最大,为4050元.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元,满足
万元,满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润![]() (万元)表示为年促销费用
(万元)表示为年促销费用![]() (万元)的函数;
(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有如下性质:如果常数
,有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)已知![]() ,
,![]() ,利用上述性质,求
,利用上述性质,求![]() 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数![]() 和函数
和函数![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的![]() 国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对
国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组对![]() 两个公司的扫码支付准备从国内
两个公司的扫码支付准备从国内![]() 个人口超过
个人口超过![]() 万的超大城市和
万的超大城市和![]() 个人口低于
个人口低于![]() 万的小城市随机抽取若干个进行统计,若一次抽取
万的小城市随机抽取若干个进行统计,若一次抽取![]() 个城市,全是小城市的概率为
个城市,全是小城市的概率为![]() .
.
(I)求![]() 的值;
的值;
(Ⅱ)若一次抽取![]() 个城市,则:
个城市,则:
①假设取出小城市的个数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②取出![]() 个城市是同一类城市求全为超大城市的概率.
个城市是同一类城市求全为超大城市的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com