
分析 根据等差数列与等比数列的定义,可判断①; 根据相关系数的意义,可判断②;根据回归直线的几何意义,可判断③;根据对勾函数的图象和性质,可判断④.
解答 解:①非零常数列既是等差数列,又是等比数列,故①为假命题;
②两个变量的相关系数的绝对值越接近于1,它们的相关性越强,故②为真命题.
③回归直线方程=$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$可以不经过点(x1,y1),(x2,y2),…,(xn,yn)中的任一个点,故③为假命题.
④函数y=sin2x+$\frac{4}{si{n}^{2}x}$(x≠kπ),在sin2x=1时,取最小值是5,故④为假命题.
故答案为:②
点评 本题以命题的真假判断与应用为载体考查了数列的定义,回归分析,相关关系,对勾函数的图象和性质等知识点,难度中档.


科目:高中数学 来源: 题型:解答题
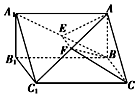 已知直三棱柱ABC-A1B1C1中,上底面是斜边为AC的直角三角形,E、F分别是A1B、AC1的中点.
已知直三棱柱ABC-A1B1C1中,上底面是斜边为AC的直角三角形,E、F分别是A1B、AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
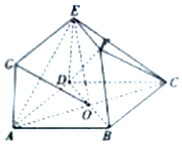 如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,四边形ADEG是平行四边形,O为正方形ABCD的中心,AB=$\sqrt{2}$,EF∥BD,DE=EF=1,DE⊥BD.
如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,四边形ADEG是平行四边形,O为正方形ABCD的中心,AB=$\sqrt{2}$,EF∥BD,DE=EF=1,DE⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4或-3 | B. | 4或-3或1 | C. | 1或3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com