
分析 求出函数的导函数,对二次项系数分类讨论,确定导函数的正负,得出原函数的单调性,求出在闭区间上函数的最大值即可.
解答 解:由题意,f′(x)=-3mx2+3,
当m≤0时-3mx2+3>0,函数是增函数,f(1)=3-m,只需f(1)≤1即可,解得m≥2,不成立,
当m>0时,令f′(x)=-3mx2+3=0解得x=±$\frac{\sqrt{m}}{m}$,
①当x<-$\frac{\sqrt{m}}{m}$或x>$\frac{\sqrt{m}}{m}$ 时,f′(x)<0,f(x)为递减函数,
②当-$\frac{\sqrt{m}}{m}$≤x≤$\frac{\sqrt{m}}{m}$时,f′(x)>0,f(x)为递增函数,
∵函数为奇函数,
∴x∈[-1,1],f(x)的最大值为f(1)或f($\frac{\sqrt{m}}{m}$)或f(-1),
∴f(1)≤1,得m≥2,f(-1)≤1,得m≤4,
f($\frac{\sqrt{m}}{m}$)≤1得,m≥4,
综上a=4为所求.
故答案为:4.
点评 考查了导函数的分类讨论,确定原函数的单调性问题和恒成立问题的转换.


科目:高中数学 来源: 题型:填空题
 如图所示的几何体是由正四棱锥和圆柱组合而成,且该几何体内接于球(正四棱锥的顶点都在球面上),正四棱锥底面边长为2,体积为$\frac{4}{3}$,则圆柱的体积为2π.
如图所示的几何体是由正四棱锥和圆柱组合而成,且该几何体内接于球(正四棱锥的顶点都在球面上),正四棱锥底面边长为2,体积为$\frac{4}{3}$,则圆柱的体积为2π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都不为0 | B. | 假设a,b,c中至少有两个为0 | ||
| C. | 假设a,b,c中至多有两个为0 | D. | 假设a,b,c中至多有一个为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
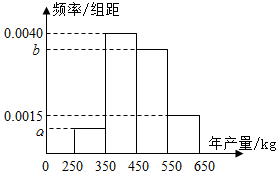 某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com