
分析 (1)由an+1-3n+2=2(an-3n+1),得到{an-3n+1}是以-8为首项,以2为公比的等比数列;
(2)由(1)可知,an-3n+1=-8×2n-1=-2n+2,即可出答案.
(3)an+1=2an+3•2n-1,两边同时除以2n+1,得到{$\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{1}{2}$为首项,以$\frac{3}{4}$为首项的等差数列,即可出答案.
解答 解:(1)数列{an}满足a1=1,an+1=2an+3n+1.
∴an+1-3n+2=2(an-3n+1),
∵a1=1,
∴a1-31+1=1-9=-8,
∴{an-3n+1}是以-8为首项,以2为公比的等比数列;
(2)由(1)可知,an-3n+1=-8×2n-1=-2n+2,
∴an=3n+1-2n+2,
当n=1时,成立,
故an=3n+1-2n+2,
(3)∵an+1=2an+3•2n-1,两边同时除以2n+1,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$=$\frac{{a}_{n}}{{2}^{n}}$+$\frac{3}{4}$,
即$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{3}{4}$,
∵a1=1,
∴$\frac{{a}_{1}}{2}$=$\frac{1}{2}$,
∴{$\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{1}{2}$为首项,以$\frac{3}{4}$为首项的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$+$\frac{3}{4}$(n-1)=$\frac{3n}{4}$-$\frac{1}{4}$,
∴an=(3n-1)2n-2.
点评 本题考查等比数列的证明,考查数列的通项公式的求法,解题时要认真审题,注意等价转化思想的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
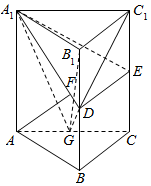 如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 84 | C. | 120 | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (12,+∞) | C. | (-∞,0) | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
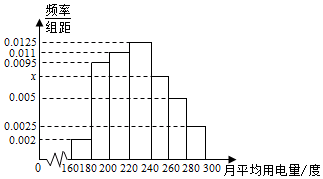 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com