
| A. | [4,+∞) | B. | (12,+∞) | C. | (-∞,0) | D. | (-∞,0] |
分析 根据函数的表达式可判断函数为奇函数,且单调递增.不等式可整理为(x+1)(x-1)(x-6)<-m恒成立,只需构造函数h(x)=(x+1)(x-1)(x-6),求出区间内的最大值即可.因为x∈(1,2],故能取等号.
解答 解:∵f(x)=1g(x+$\sqrt{{x}^{2}+1}$),
∴f(-x)=1g(-x+$\sqrt{{x}^{2}+1}$)
=-f(x),
∴函数为奇函数,由表达式显然知函数为增函数,
∵f($\frac{x+1}{x-1}$)+f[$\frac{m}{(x-1)^{2}(x-6)}$]>0恒成立,
∴$\frac{x+1}{x-1}$>-$\frac{m}{(x-1)^{2}(x-6)}$,
∴(x+1)(x-1)(x-6)<-m恒成立,
令h(x)=(x+1)(x-1)(x-6),可知函数h(x)在x∈(1,2]时,单调递减,
∴h(x)的最大值大于h(1)=0,
∴0≤-m,
∴m≤0,
故选:D.
点评 本题考查了函数的奇偶性和单调性和应用,利用构造函数的方法,通过求函数的最值解决恒成立问题.


科目:高中数学 来源: 题型:填空题
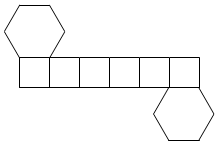 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都不为0 | B. | 假设a,b,c中至少有两个为0 | ||
| C. | 假设a,b,c中至多有两个为0 | D. | 假设a,b,c中至多有一个为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{51}{70}$ | B. | $\frac{70}{51}$ | C. | $\frac{35}{17}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
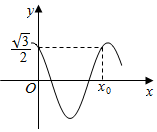 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )| A. | $φ=\frac{π}{6},{x_0}=\frac{5}{3}$ | B. | $φ=\frac{π}{6},{x_0}=1$ | C. | $φ=\frac{π}{3},{x_0}=\frac{5}{3}$ | D. | $φ=\frac{π}{3},{x_0}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com