
分析 设直线l的方程,代入椭圆方程,由韦达定理,弦长公式及中点坐标公式,求得中点坐标Q坐标,求得MN垂直平分线方程,当y=0时,即可求得P点坐标,代入即可求得丨PF丨,即可求得$\frac{|MN|}{|PF|}$,即可求得a和c的关系,即可求得椭圆的离心率.
解答 解:设直线l的方程为:y=(x-c)(k≠0),M(x1,y1),N(x2,y2),
线段MN的中点Q(x0,y0).
联立$\left\{\begin{array}{l}{y=x-c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为(a2+b2)x2-2a2cx+a2c2-a2b2=0,
∴x1+x2=$\frac{2{a}^{2}c}{{a}^{2}+{b}^{2}}$,x1x2=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$.
∴|MN|=$\sqrt{1+{1}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{4a{b}^{2}}{{a}^{2}+{b}^{2}}$,x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{{a}^{2}c}{{a}^{2}+{b}^{2}}$.
∴y0=x0-c=-$\frac{{b}^{2}c}{{a}^{2}+{b}^{2}}$,
∴MN的垂直平分线为:y+$\frac{{b}^{2}c}{{a}^{2}+{b}^{2}}$=-(x-$\frac{{a}^{2}c}{{a}^{2}+{b}^{2}}$),
令y=0,解得xP=$\frac{{c}^{3}}{{a}^{2}+{b}^{2}}$,
∴P($\frac{{c}^{3}}{{a}^{2}+{b}^{2}}$,0).
∴|PF|=c-xP=$\frac{{2b}^{2}c}{{a}^{2}+{b}^{2}}$,
∴$\frac{|MN|}{|PF|}$=$\frac{2a}{c}$=4,
则$\frac{c}{a}$=$\frac{1}{2}$,
∴椭圆C的离心率$\frac{1}{2}$,
当k=0时,$\frac{|MN|}{|PF|}$=,也成立,
∴椭圆C的离心率$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查简单几何性质,考查直线与椭圆的位置关系,考查直线的垂直平分线的求法,考查计算能力,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
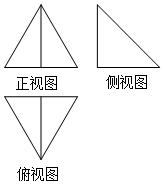 一个简单几何体的三视图如图所示,其正视图和俯视图均为正三角形,侧视图为腰长是2的等腰直角三角形则该几何体的体积为( )
一个简单几何体的三视图如图所示,其正视图和俯视图均为正三角形,侧视图为腰长是2的等腰直角三角形则该几何体的体积为( )| A. | $\frac{4}{9}$$\sqrt{3}$ | B. | 1 | C. | $\frac{8}{9}$$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | 4 | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com