
分析 (1)令f(x)=(1+x)t-tx-1,求导数,当t>1时,(1+x)t-1-1单调递增,讨论在x>-1时,求出单调增区间和单调减区间,得到x=0是f(x)的唯一极小值点,则f(x)≥(0)=0,即可得证;
(2)分a=b和a≠b两种情况证明结论,并构造函数φ(x)=xa-xb,先证得φ(x)是单调减函数,进而得到结论.
解答 证明:(1)令f(x)=(1+x)t-1-tx,f′(x)=t[(1+x)t-1-1],
∵t>1,∴t-1>0,
x∈(-1,0]时,(1+x)t-1≤1,f′(x)≤0,函数单调递减;x>0时,f′(x)>0,函数单调递增,
∴x=0是f(x)的唯一极小值点,
∴f(x)≥f(0)=0,
即:(1+x)t≥1+tx;
(2)当a=b,不等式显然成立;
当a≠b时,不妨设a<b,
则aa+bb≥ab+ba?aa-ab≥ba-bb,
令φ(x)=xa-xb,x∈[a,b]
下证φ(x)是单调减函数.
∵φ′(x)=axa-1-bxb-1=axb-1(xa-b-$\frac{b}{a}$)
易知a-b∈(-1,0),1+a-b∈(0,1),$\frac{1}{1+a-b}$>1,
由(1)知当t>1,(1+x)t>1+tx,x∈[a,b],
∴${b}^{\frac{1}{1+a-b}}$=$[1+(b-1)]^{\frac{1}{1+a-b}}$>1+$\frac{b-1}{1+a-b}$=$\frac{a}{1+a-b}$>a,
∴b>a1+a-b,∴$\frac{b}{a}$>aa-b≥xa-b,
∴φ'(x)<0,
∴φ(x)在[a,b]上单调递减.
∴φ(a)>φ(b),
即aa-ab>ba-bb,
∴aa+bb>ab+ba.
综上,aa+bb≥ab+ba成立.
点评 考查不等式的证明,考查运用导数判断函数的单调性,证明不等式的方法,构造函数是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | $(-1,\frac{7}{2})$ | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
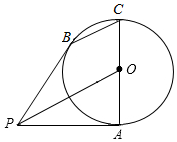 如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com