
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
分析 确定函数是周期为2的周期函数,f(x)在[0,1]上单调递增,并且a=f(log0.52)=f(log22)=f(1),b=f(log24)=f(2)=f(0),c=f(20.5),即可比较出a,b,c的大小.
解答 解:∵f(x+2)=f(x),
∴函数是周期为2的周期函数;
∵f(x)为偶函数,f(x)在[-1,0]上是减函数,
∴f(x)在[0,1]上单调递增,
并且a=f(log0.52)=f(log22)=f(1),b=f(log24)=f(2)=f(0),
c=f(20.5)=f(2-20.5).
∵0<2-20.5<1,
∴b<c<a.
故选:C.
点评 考查偶函数的定义,函数的单调性,对于偶函数比较函数值大小的方法就是将自变量的值变到区间[0,1]上,根据单调性去比较函数值大小.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 恒小于0 | B. | 恒大于0 | C. | 等于0 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5或2 | B. | -1或4 | C. | -5或4 | D. | -5或-1或2或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
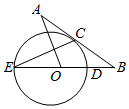 如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.
如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com