
分析 (I)使用两角和差的三角函数公式化简f(x),根据正弦函数的单调区间列出不等式解出;
(II)求出B,利用余弦定理列方程得出.
解答 解:(Ⅰ)f(x)=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x-$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}$sin2x-$\sqrt{3}$cos2x=si2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$).
令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2}$,解得$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12}$,
∴f(x)的单调递增区间为$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]\;({k∈Z})$.
(Ⅱ)∵$f(B)=\sqrt{3}$,∴$sin({2B-\frac{π}{3}})=\frac{{\sqrt{3}}}{2}$
∵$0<B<\frac{π}{2}$,∴$-\frac{π}{3}<2B-\frac{π}{3}<\frac{2π}{3}$,
∴$2B-\frac{π}{3}=\frac{π}{3}$,∴$B=\frac{π}{3}$.
∴$cosB=\frac{{A{B^2}+B{C^2}-A{C^2}}}{2AB•BC}=\frac{1}{2}$,
又 $AC=\sqrt{3}$,△ABC的周长为$3\sqrt{3}$.
∴$AB+BC=2\sqrt{3}$,AB•BC=3,
解得$AB=\sqrt{3}$,$BC=\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,正弦函数的性质,余弦定理,属于中档题.


科目:高中数学 来源: 题型:填空题
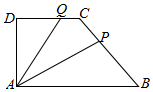 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com