
分析 (1)根据题意,分2步进行分析:第一步:让女生甲站排头或排尾,第二步:剩余6人站其它6个位置,进行全排列即可,由分步计数原理计算可得答案;
(2)根据题意,分2步进行分析:第一步:从中间5个位置选2个站两个女生,第二步:剩余5人站其它5个位置,将5人进行全排列即可,由分步计数原理计算可得答案;
(3)根据题意,分2步进行分析:第一步:将5个男生进行排列,第二步:从6个空中选2个给两名女生排列,求出每一步的情况数目,由分步计数原理计算可得答案;
(4)根据题意,首先将7人站成一排进行全排列,由于女生甲在女生乙右方和左方的排法数目相同,由倍分法计算可得答案.
解答 解:(1)根据题意,分2步进行分析:
第一步:让女生甲站排头或排尾,有2种站法;
第二步:剩余6人站其它6个位置,共有$A_6^6$种站法.
由分步计数原理得,女生甲站两端,共有$2×A_6^6=1440$种站法.
(2)根据题意,分2步进行分析:
第一步:从中间5个位置选2个站两个女生,有$A_5^2=20$种站法;
第二步:剩余5人站其它5个位置,有A55=120种站法.
由分步计数原理得,两个女生都不站在两端共有A52A55=2400种站法.
(3)根据题意,分2步进行分析:
第一步:将5个男生进行排列,有A55种站法;
第二步:从6个空中选2个给两名女生排列,有A62种站法.
由分步计数原理得,两个女生不相邻有A55A62=3600种站法.
(4)7人站成一排,有A77种排法,
由于女生甲在女生乙右方和左方的可能性相同,即排法数目相同,
故共有$\frac{{A}_{7}^{7}}{2}$=2520种站法.
点评 本题考查排列、组合的运用,涉及分类、分步计数原理原理的应用,注意常见问题的处理方法.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
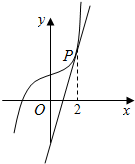 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com