
分析 (1)由题意求出a利用新定义求出b,即可求解椭圆C的方程.
(2)①当直线l为:y=0,验证是否符合题意;②当直线l不在x轴上时,由(1)知F2为(1,0),设l为:x=my+1,将其代入椭圆C的方程利用韦达定理以及弦长公式,通过三角形的面积,求出m,得到直线方程.
解答 解:(1)由题意:2a=4⇒a=2,$\overrightarrow{OA}?\overrightarrow{OB}=absin{90°}=ab=2\sqrt{3}$,
∴$b=\sqrt{3}$,∴所求椭圆C为:$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)①当直线l为:y=0,即在x轴上时,$\overrightarrow{OM}?\overrightarrow{ON}=|{\overrightarrow{OM}}||{\overrightarrow{ON}}|sin{180°}=0≠\frac{{12\sqrt{2}}}{7}$不符合题意;
②当直线l不在x轴上时,由(1)知F2为(1,0),
设l为:x=my+1,将其代入椭圆C的方程得:(3m2+4)x2+6my-9=0,
∴$\left\{{\begin{array}{l}{{y_1}+{y_2}=-\frac{6m}{{3{m^2}+4}}}\\{{y_1}{y_2}=-\frac{9}{{3{m^2}+4}}}\end{array}}\right.$,
∴$|{{y_1}-{y_2}}|=\sqrt{({y_1}+{y_2}{)^2}-4{y_1}{y_2}}=\sqrt{\frac{{36{m^2}}}{{{{(3{m^2}+4)}^2}}}+\frac{36}{{3{m^2}+4}}}=\frac{{12\sqrt{{m^2}+1}}}{{3{m^2}+4}}$,
又$\overrightarrow{OM}?\overrightarrow{ON}=|{\overrightarrow{OM}}||{\overrightarrow{ON}}|sin<\overrightarrow{OM},\overrightarrow{ON}>=2{S_{△OAB}}$=$2×\frac{1}{2}×|{O{F_2}}|×|{{y_1}-{y_2}}|=|{{y_1}-{y_2}}|=\frac{{12\sqrt{{m^2}+1}}}{{3{m^2}+4}}=\frac{{12\sqrt{2}}}{7}$,
解得:m2=1或${m^2}=-\frac{17}{18}$(舍去),即m=±1.
综上,直线l的方程为:y=x-1或y=-x+1.
点评 本题考查椭圆的方程的求法,椭圆的简单性质的应用,直线与椭圆的位置关系的应用,考查计算能力.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
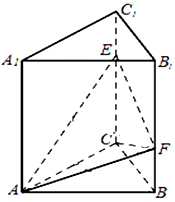 如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.
如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
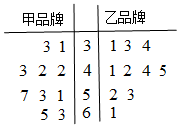 某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | (-1,1) | C. | [-1,1] | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com