
���� ��1������C2��$��=2\sqrt{2}cos����+\frac{��}{4}��$�����Ի�Ϊ${��^2}=2\sqrt{2}��cos����+\frac{��}{4}��$����2=2��cos��-2��sin�ȣ��ɵ�����C��ֱ�����귽�̣���ָ�����ʾ�������ߣ�
��2����$��=\frac{��}{4}$ʱ��ֱ�ߵIJ�������Ϊ$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��Ϊ�����������ò����ļ���������$��=\frac{��}{4}$ʱ��|PA|+|PB|��ֵ��
��� �⣺��1������C2��$��=2\sqrt{2}cos����+\frac{��}{4}��$�����Ի�Ϊ${��^2}=2\sqrt{2}��cos����+\frac{��}{4}��$����2=2��cos��-2��sin�ȣ�
��ˣ�����C��ֱ�����귽��Ϊx2+y2-2x+2y=0����4�֣�
����ʾ�ԣ�1��-1��ΪԲ�ġ�$\sqrt{2}$Ϊ�뾶��Բ���� ����5�֣�
��2����$��=\frac{��}{4}$ʱ��ֱ�ߵIJ�������Ϊ$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��Ϊ������
��P��1��0����ֱ���ϣ�����ԲC�ڣ���$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$
����x2+y2-2x+2y=0�е�${t^2}+\sqrt{2}t-1=0$����6�֣�
������ʵ����Ϊt1��t2����A��B��������Ӧ�IJ���Ϊt1��t2��
��${t_1}+{t_2}=-\sqrt{2}$��t1t2=-1����8�֣���$|PA|+|PB|=|{t_1}-{t_2}|=\sqrt{{{��{t_1}+{t_2}��}^2}-4{t_1}{t_2}}=\sqrt{6}$����10�֣�
���� ���⿼�鼫���귽����ֱ�����귽�̵Ļ���������������̵����ã������е��⣮


 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{12}$ | B�� | $-\frac{��}{12}$ | C�� | $\frac{��}{4}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
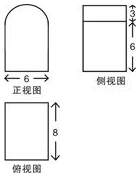 ��֪ij�����������ͼ��ͼ��ʾ������ͼ�Ļ����ǰ�Բ��������ͼ�б�������ݣ����������ı�����ǣ�������
��֪ij�����������ͼ��ͼ��ʾ������ͼ�Ļ����ǰ�Բ��������ͼ�б�������ݣ����������ı�����ǣ�������| A�� | 36��+288 | B�� | 36��+216 | C�� | 33��+288 | D�� | 33��+216 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{3}{4}��p��\frac{7}{8}$ | B�� | $p��\frac{5}{16}$ | C�� | $\frac{7}{8}��p��\frac{5}{16}$ | D�� | $\frac{7}{8}��p��\frac{5}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
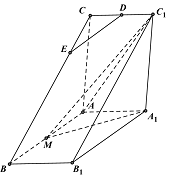 ��ͼ��ֱ������ABC-A1B1C1�У�AC��AB��AB=2AA��M��AB���е㣬��A1MC1�ǵ��������Σ�DΪCC1���е㣬EΪBC��һ�㣮
��ͼ��ֱ������ABC-A1B1C1�У�AC��AB��AB=2AA��M��AB���е㣬��A1MC1�ǵ��������Σ�DΪCC1���е㣬EΪBC��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com