
已知△ABC中,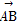 =a,
=a,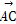 =b,对于平面ABC上任意一点O,动点P满足
=b,对于平面ABC上任意一点O,动点P满足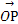 =
=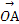 +λa+λb,则动点P的轨迹所过的定点为 .
+λa+λb,则动点P的轨迹所过的定点为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
若点A(3,5)关于直线l:y=kx的对称点在x轴上,则k是( )
(A) (B)±
(B)±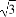
(C)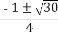 (D)
(D)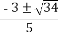
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:填空题
已知向量a=(-2,3),b∥a,向量b的起点为A(1,2),终点B在坐标轴上,则点B的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:选择题
已知圆O(O为坐标原点)的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么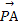 ·
·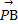 的最小值为( )
的最小值为( )
(A)-4+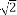 (B)-3+
(B)-3+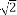
(C)-4+2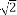 (D)-3+2
(D)-3+2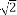
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:选择题
设P是曲线y=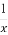 上一点,点P关于直线y=x的对称点为Q,点O为坐标原点,则
上一点,点P关于直线y=x的对称点为Q,点O为坐标原点,则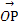 ·
·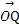 =( )
=( )
(A)0(B)1(C)2(D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
已知点P为△ABC所在平面上的一点,且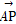 =
=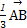 +t
+t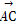 ,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )
,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )
(A)0<t< (B)0<t<
(B)0<t< (C)0<t<
(C)0<t< (D)0<t<
(D)0<t<
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
在以下各命题中,假命题的个数为( )
①“|a|=|b|”是“a=b”的必要不充分条件
②任一非零向量的方向都是唯一的
③“a∥b”是“a=b”的充分不必要条件
④若|a|-|b|=|a|+|b|,则b=0
(A)1(B)2(C)3(D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十九第四章第五节练习卷(解析版) 题型:解答题
已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数满足| -a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
已知向量a=(cosθ,sinθ),b=(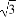 ,-1),则|2a-b|的最大值为( )
,-1),则|2a-b|的最大值为( )
(A)4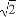 (B)4(C)16(D)8
(B)4(C)16(D)8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com