
ЎҫМвДҝЎҝИфКэБР![]() УләҜКэ
УләҜКэ![]() ВъЧгЈәўЩ
ВъЧгЈәўЩ![]() өДИОТвБҪПоҫщІ»ПаөИЈ¬ЗТ
өДИОТвБҪПоҫщІ»ПаөИЈ¬ЗТ![]() өД¶ЁТеУтОӘ
өД¶ЁТеУтОӘ![]() Ј»ўЪКэБР
Ј»ўЪКэБР![]() өДЗ°
өДЗ°![]() өДПоөДәН
өДПоөДәН![]() ¶ФИОТвөД
¶ФИОТвөД![]() ¶јіЙБўЈ¬ФтіЖ
¶јіЙБўЈ¬ФтіЖ![]() Ул
Ул![]() ҫЯУРЎ°№ІЙъ№ШПөЎұЈ®
ҫЯУРЎ°№ІЙъ№ШПөЎұЈ®
ЈЁ1Ј©Иф![]() Ј¬КФРҙіцТ»ёцУлКэБР
Ј¬КФРҙіцТ»ёцУлКэБР![]() ҫЯУРЎ°№ІЙъ№ШПөЎұөДәҜКэ
ҫЯУРЎ°№ІЙъ№ШПөЎұөДәҜКэ![]() өДҪвОцКҪЈ»
өДҪвОцКҪЈ»
ЈЁ2Ј©Иф![]() УлКэБР
УлКэБР![]() ҫЯУРЎ°№ІЙъ№ШПөЎұЈ¬ЗуКөКэ¶Ф
ҫЯУРЎ°№ІЙъ№ШПөЎұЈ¬ЗуКөКэ¶Ф![]() Лщ№№іЙөДјҜәПЈ¬ІўРҙіц
Лщ№№іЙөДјҜәПЈ¬ІўРҙіц![]() №ШУЪ
№ШУЪ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() өДұнҙпКҪЈ»
өДұнҙпКҪЈ»
ЈЁ3Ј©Иф![]() Ј¬ЗуЦӨЈәЎ°ҙжФЪГҝПо¶јКЗХэКэөДОЮЗоөИІоКэБР
Ј¬ЗуЦӨЈәЎ°ҙжФЪГҝПо¶јКЗХэКэөДОЮЗоөИІоКэБР![]() Ј¬К№өГ
Ј¬К№өГ![]() Ул
Ул![]() ҫЯУРЎ®№ІЙъ№ШПөЎҜЎұөДідТӘМхјюКЗЎ°өг
ҫЯУРЎ®№ІЙъ№ШПөЎҜЎұөДідТӘМхјюКЗЎ°өг![]() ФЪЙдПЯ
ФЪЙдПЯ![]() ЙПЎұЈ®
ЙПЎұЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() ЈЁ2Ј©КөКэ¶Ф
ЈЁ2Ј©КөКэ¶Ф![]() Лщ№№іЙөДјҜәПОӘ
Лщ№№іЙөДјҜәПОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ј¬
Ј¬ . ЈЁ3Ј©ЦӨГчјыҪвОц.
. ЈЁ3Ј©ЦӨГчјыҪвОц.
ЎҫҪвОцЎҝ
(1) УЙ![]() Ј¬ҝЙЦӘ
Ј¬ҝЙЦӘ![]() Ј¬ҙУ¶шҝЙөГ
Ј¬ҙУ¶шҝЙөГ![]() .
.
(2) УЙМвТвөГ![]() ,өұ
,өұ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬Ул
КұЈ¬Ул![]() өДИОТвБҪПоҫщІ»ПаөИПаГ¬¶Ь,№КҙЛКұІ»әПМвТвЈ»өұ
өДИОТвБҪПоҫщІ»ПаөИПаГ¬¶Ь,№КҙЛКұІ»әПМвТвЈ»өұ![]() Ј¬
Ј¬![]() Ј¬І»әПМвТвЈ¬өұ
Ј¬І»әПМвТвЈ¬өұ![]() Ј¬ТІІ»әПМвТв. Иф
Ј¬ТІІ»әПМвТв. Иф![]() Ј¬Фт
Ј¬Фт![]() Ј¬УЙ
Ј¬УЙ![]() Ј¬
Ј¬![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬
Ј¬![]() өДИОТвБҪПоҫщІ»ПаөИЈ¬№К
өДИОТвБҪПоҫщІ»ПаөИЈ¬№К![]() Ј¬ҝЙЦӘ
Ј¬ҝЙЦӘ![]() Ј¬өГіцҙр°ё.
Ј¬өГіцҙр°ё.
(3)ПИЦӨұШТӘРФЈ¬Иф![]() КЗ
КЗ![]() №«ІоөДөИІоКэБРЈ¬
№«ІоөДөИІоКэБРЈ¬![]()
![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬№К
Ј¬№К ҪвөГ
ҪвөГ![]() Ј¬ФЩЦӨід·ЦРФЈ¬Ифөг
Ј¬ФЩЦӨід·ЦРФЈ¬Ифөг![]() ФЪЙдПЯ
ФЪЙдПЯ![]() ЙПЈ¬
ЙПЈ¬![]()
јҙ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬ҙУ¶шөГЦӨ.
Ј¬ҙУ¶шөГЦӨ.
(1)УЙ![]() Ј¬ҝЙЦӘ
Ј¬ҝЙЦӘ![]()
ЛщТФУлКэБР![]() ҫЯУРЎ°№ІЙъ№ШПөЎұөДәҜКэ
ҫЯУРЎ°№ІЙъ№ШПөЎұөДәҜКэ![]() өДҪвОцКҪҝЙТФОӘЈә
өДҪвОцКҪҝЙТФОӘЈә![]() .
.
(2)УЙМвТвөГ![]() Ј¬Бо
Ј¬Бо![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬јҙ
Ј¬јҙ![]() .
.
ўЩИф![]() Ј¬ҙЛКұІ»іЙБўЈ¬І»әПМвТвЈ¬
Ј¬ҙЛКұІ»іЙБўЈ¬І»әПМвТвЈ¬
Иф![]() Ј¬УЙ
Ј¬УЙ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬УЦ
Ј¬УЦ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬Ул
Ј¬Ул![]() өДИОТвБҪПоҫщІ»ПаөИПаГ¬¶Ь,№КҙЛКұІ»әПМвТв.
өДИОТвБҪПоҫщІ»ПаөИПаГ¬¶Ь,№КҙЛКұІ»әПМвТв.
ўЪИф![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]()
Иф![]() Ј¬ФтУЙ
Ј¬ФтУЙ![]() Ул
Ул![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬І»әПМвТв.
Ј¬І»әПМвТв.
Иф![]() Ј¬Фт
Ј¬Фт![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬
КұЈ¬![]() Ј¬І»әПМвТв.
Ј¬І»әПМвТв.
Иф![]() Ј¬Фт
Ј¬Фт![]() Ј¬УЙ
Ј¬УЙ![]() Ј¬
Ј¬![]()
ҝЙөГ![]() Ј¬јҙ
Ј¬јҙ![]()
ҙЛКұКэБР![]() КЗКЧПоОӘ
КЗКЧПоОӘ![]() Ј¬№«ұИОӘ
Ј¬№«ұИОӘ![]() өДөИұИКэБРЈ¬УЦ
өДөИұИКэБРЈ¬УЦ![]() өДИОТвБҪПоҫщІ»ПаөИЈ¬
өДИОТвБҪПоҫщІ»ПаөИЈ¬
№К![]() Ј¬ҝЙЦӘ
Ј¬ҝЙЦӘ![]()
ЛщТФКөКэ¶Ф![]() Лщ№№іЙөДјҜәПОӘ
Лщ№№іЙөДјҜәПОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]()

(3)(ұШТӘРФ)Иф![]() КЗ
КЗ![]() №«ІоөДөИІоКэБРЈ¬ЗТУл
№«ІоөДөИІоКэБРЈ¬ЗТУл![]() ҫЯУРЎ°№ІЙъ№ШПөЎұ.
ҫЯУРЎ°№ІЙъ№ШПөЎұ.
ФтУЙ![]() Ј¬
Ј¬![]()
ҝЙөГ: ![]()
№К![]() Ј¬јҙ
Ј¬јҙ![]() әгіЙБў.
әгіЙБў.
№К ҪвөГ
ҪвөГ![]()
УЦУЙ![]() ,ҝЙөГ
,ҝЙөГ![]() ,
,
УЙ![]() ,ҝЙЦӘ
,ҝЙЦӘ![]()
ЛщТФөг![]() ФЪЙдПЯ
ФЪЙдПЯ![]() ЙП.
ЙП.
(ід·ЦРФ)Ифөг![]() ФЪЙдПЯ
ФЪЙдПЯ![]() ЙПЈ¬Фт
ЙПЈ¬Фт![]()
УЦ·ҪіМ![]() өИјЫУЪ
өИјЫУЪ![]() Ј¬
Ј¬![]()
ЗТ![]() Ј¬ИЎ
Ј¬ИЎ![]() Ј¬ЛьПФИ»КЗХэКэЗТВъЧг
Ј¬ЛьПФИ»КЗХэКэЗТВъЧг![]()
Бо![]() Ј¬Фт
Ј¬Фт![]()
![]() Ј¬
Ј¬
№Көұ![]() КұЈ¬
КұЈ¬![]()
ХвАпОЮЗоКэБР![]() КЗКЧПоОӘ
КЗКЧПоОӘ![]() Ј¬№«ІоОӘ
Ј¬№«ІоОӘ![]() өДОЮЗоөИІоКэБР.
өДОЮЗоөИІоКэБР.
ЖдЦРГҝТ»По¶јКЗХэКэЈ¬ЛщТФҙжФЪГҝТ»По¶јКЗХэКэөДОЮЗоөИІоКэБР![]() Ј¬К№өГ
Ј¬К№өГ![]() Ул
Ул![]() ҫЯУРЎ°№ІЙъ№ШПөЎұ.
ҫЯУРЎ°№ІЙъ№ШПөЎұ.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬БвРО![]() өДұЯіӨОӘ12Ј¬
өДұЯіӨОӘ12Ј¬![]() Ј¬
Ј¬![]() Ул
Ул![]() Ҫ»УЪ
Ҫ»УЪ![]() өгЈ¬Ҫ«БвРО
өгЈ¬Ҫ«БвРО![]() СШ¶ФҪЗПЯ
СШ¶ФҪЗПЯ![]() ХЫЖрЈ¬өГөҪИэАвЧ¶
ХЫЖрЈ¬өГөҪИэАвЧ¶![]() Ј¬өг
Ј¬өг![]() КЗАв
КЗАв![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]() Ј®
Ј®
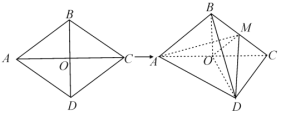
ЈЁ1Ј©ЗуЦӨЈә![]() Ј»
Ј»
ЈЁ2Ј©Зу¶юГжҪЗ![]() өДУаПТЦөЈ®
өДУаПТЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯ![]() өДІОКэ·ҪіМОӘ
өДІОКэ·ҪіМОӘ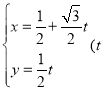 ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬
ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬![]() ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() .
.
ЈЁ1Ј©ЗуЦұПЯ![]() өДЖХНЁ·ҪіМәНЗъПЯ
өДЖХНЁ·ҪіМәНЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©Йиөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°Јј°ҪрЧЦЛюКЗ№Е°Јј°өДөЫНхЈЁ·ЁАПЈ©БкД№Ј¬КАҪзЖЯҙуЖжјЈЦ®Т»Ј¬ЖдЦРҪПОӘЦшГыөДКЗәъ·тҪрЧЦЛюЈ®БоИЛіФҫӘөДІўІ»ҪцҪцКЗәъ·тҪрЧЦЛюөДРЫЧіЙнЧЛЈ¬»№УР·ўЙъФЪәъ·тҪрЧЦЛюЙПөДКэЧЦЎ°ЗЙәПЎұЈ®Изәъ·тҪрЧЦЛюөДөЧІҝЦЬіӨИз№ыіэТФЖдёЯ¶ИөДБҪұ¶Ј¬өГөҪөДЙМОӘ3.14159Ј¬ХвҫНКЗФІЦЬВКҪПОӘҫ«И·өДҪьЛЖЦөЈ®ҪрЧЦЛюөЧІҝРООӘХэ·ҪРОЈ¬ХыёцЛюРООӘХэЛДАвЧ¶Ј¬ҫӯ№ЕҙъДЬ№ӨЗЙҪіҪЁЙиНкіЙәуЈ¬өЧЧщұЯіӨҙуФј230ГЧЈ®ТтДкҫГ·з»ҜЈ¬¶Ҙ¶Л°юВд10ГЧЈ¬Фтәъ·тҪрЧЦЛюПЦёЯҙуФјОӘЈЁ Ј©
A.128.5ГЧB.132.5ГЧC.136.5ГЧD.110.5ГЧ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЗъПЯ
ЦРЈ¬ЗъПЯ![]() №эөг
№эөг![]() Ј¬ЖдІОКэ·ҪіМОӘ
Ј¬ЖдІОКэ·ҪіМОӘ ЈЁ
ЈЁ![]() ОӘІОКэЈ¬
ОӘІОКэЈ¬![]() Ј©Ј¬ТФ
Ј©Ј¬ТФ![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬![]() Цб·Зёә°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
Цб·Зёә°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() .
.
ЈЁ1Ј©ЗуЗъПЯ![]() өДЖХНЁ·ҪіМәНЗъПЯ
өДЖХНЁ·ҪіМәНЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©ЗуТСЦӘЗъПЯ![]() әНЗъПЯ
әНЗъПЯ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬ЗТ
БҪөгЈ¬ЗТ![]() Ј¬ЗуКөКэ
Ј¬ЗуКөКэ![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЕЧОпПЯ![]() өД¶ҘөгКЗНЦФІ
өД¶ҘөгКЗНЦФІ![]() өДЦРРДЈ¬Ҫ№өгУлёГНЦФІөДУТҪ№өгЦШәП.
өДЦРРДЈ¬Ҫ№өгУлёГНЦФІөДУТҪ№өгЦШәП.
ЈЁ1Ј©ЗуЕЧОпПЯ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ТСЦӘ¶ҜЦұПЯ![]() №эөг
№эөг![]() Ј¬Ҫ»ЕЧОпПЯ
Ј¬Ҫ»ЕЧОпПЯ![]() УЪ
УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬ЧшұкФӯөг
БҪөгЈ¬ЧшұкФӯөг![]() ОӘ
ОӘ![]() өДЦРөгЈ¬ЗуЦӨ
өДЦРөгЈ¬ЗуЦӨ![]() Ј»
Ј»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬КЗ·сҙжФЪҙ№ЦұУЪ![]() ЦбөДЦұПЯ
ЦбөДЦұПЯ![]() ұ»ТФ
ұ»ТФ![]() ОӘЦұҫ¶өДФІЛщҪШөГөДПТіӨәгОӘ¶ЁЦөЈҝИз№ыҙжФЪЈ¬Зуіц
ОӘЦұҫ¶өДФІЛщҪШөГөДПТіӨәгОӘ¶ЁЦөЈҝИз№ыҙжФЪЈ¬Зуіц![]() өД·ҪіМЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
өД·ҪіМЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() №эөг
№эөг![]() Ј¬ЗТЛьөДТ»ёцҪ№өгУлЕЧОпПЯ
Ј¬ЗТЛьөДТ»ёцҪ№өгУлЕЧОпПЯ![]() өДҪ№өгПаН¬Ј®ЦұПЯ
өДҪ№өгПаН¬Ј®ЦұПЯ![]() №эөг
№эөг![]() Ј¬ЗТУлНЦФІ
Ј¬ЗТУлНЦФІ![]() ПаҪ»УЪ
ПаҪ»УЪ![]() БҪөгЈ®
БҪөгЈ®
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ИфЦұПЯ![]() өДТ»ёц·ҪПтПтБҝОӘ
өДТ»ёц·ҪПтПтБҝОӘ![]() Ј¬Зу
Ј¬Зу![]() өДГж»эЈЁЖдЦР
өДГж»эЈЁЖдЦР![]() ОӘЧшұкФӯөгЈ©Ј»
ОӘЧшұкФӯөгЈ©Ј»
ЈЁ3Ј©КФОКЈәФЪ![]() ЦбЙПКЗ·сҙжФЪөг
ЦбЙПКЗ·сҙжФЪөг![]() Ј¬К№өГ
Ј¬К№өГ![]() ОӘ¶ЁЦөЈҝИфҙжФЪЈ¬Зуіцөг
ОӘ¶ЁЦөЈҝИфҙжФЪЈ¬Зуіцөг![]() өДЧшұкәН¶ЁЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өДЧшұкәН¶ЁЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІCЈә![]() өД¶МЦбіӨОӘ2Ј¬АлРДВКОӘ
өД¶МЦбіӨОӘ2Ј¬АлРДВКОӘ![]() Ј¬Чу¶ҘөгОӘAЈ¬№эөгAөДЦұПЯlУлCҪ»УЪБнТ»ёцөгMЈ¬ЗТУлЦұПЯxЈҪtҪ»УЪөгNЈ®
Ј¬Чу¶ҘөгОӘAЈ¬№эөгAөДЦұПЯlУлCҪ»УЪБнТ»ёцөгMЈ¬ЗТУлЦұПЯxЈҪtҪ»УЪөгNЈ®
ЈЁ1Ј©ЗуНЦФІCөД·ҪіМЈ»
ЈЁ2Ј©КЗ·сҙжФЪКөКэtЈ¬К№өГ![]() ОӘ¶ЁЦөЈҝИфҙжФЪЈ¬ЗуКөКэtөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
ОӘ¶ЁЦөЈҝИфҙжФЪЈ¬ЗуКөКэtөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР{an}өДёчПоҫщОӘХэКэЈ¬ЖдЗ°nПоәНSnВъЧг4SnЈҪan2+2anЈ¬nЎКN*.ЙиbnЈҪЈЁ©Ғ1Ј©nanan+1Ј¬TnОӘКэБР{bn}өДЗ°nПоәНЈ¬ФтT2nЈҪ_____.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com