练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)是定义域为R的奇函数，且x≤0时，f(x)＝2x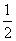－x＋a，则函数f(x)的零点个数是(　　)

    A．1  B．2  C．3  D．4


    C

    [解析]　由题意知，f(0)＝0，∴a＝－1，∴f(x)＝2x－x－1.在同一坐标系中分别作出y＝2x和y＝x＋1的图象知，当x<0时，有一解，又f(x)为奇函数．∴x>0时，有一解，又f(0)＝0，∴f(x)的零点有3个．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    双曲线的实轴长为      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若两条异面直线所成的角为60°，则称这对异面直线为“黄金异面直线对”，在连接正方体各顶点的所有直线中，“黄金异面直线对”共有(　　)

    A．12对  B．18对  C．24对  D．30对

    查看答案和解析>>

    科目：高中数学 来源： 题型：


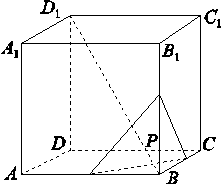
    如图，正方体ABCD－A1B1C1D1的棱长为2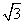，动点P在对角线BD1上，过点P作垂直于BD1的平面α，记这样得到的截面多边形(含三角形)的周长为y，设BP＝x，则当x∈[1,5]时，函数y＝f(x)的值域为(　　)

    A．[2，6]                        B．[2，18] 

    C．[3，18]                          D．[3，6]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在几何体ABC－A1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，E为AB1中点，AB＝AA1＝BB1＝2CC1.求证

    (1)CE∥平面A1B1C1；

    (2)平面AB1C1⊥平面A1BC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：

    (1)对任意a∈R，a*0＝a；

    (2)对任意a，b∈R，a*b＝ab＋(a*0)＋(b*0)．

    关于函数f(x)＝(ex)*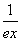的性质，有如下说法：①函数f(x)的最小值为3；②函数f(x)为偶函数；③函数f(x)的单调递增区间为(－∞，0]．

    其中所有正确说法的个数为(　　)

    A．0                                    B．1 

    C．2                                    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝(x－a)(x－b)(a>b)的图象如图所示，则函数g(x)＝ax＋b的图象是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的图象大致是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x3＋3x对任意的m∈[－2,2]，f(mx－2)＋f(x)<0恒成立，则x∈________.

    查看答案和解析>>

    同步练习册答案