
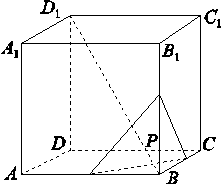
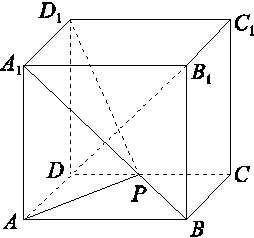
如图,正方体ABCD-A1B1C1D1的棱长为2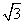 ,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
A.[2 ,6
,6 ] B.[2
] B.[2 ,18]
,18]
C.[3 ,18] D.[3
,18] D.[3 ,6
,6 ]
]
D
[解析] 当点P从点B向D1运动时,截面的周长y越来越大,当截面经过平面AB1C时,周长最大,当点P继续移动时,在截面AB1C到截面A1DC1之间,截面周长不变,当点P继续移动时,截面周长越来越小,所以截面周长的最大值就是△AB1C的周长.因为正方体的棱长为2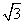 ,所以AC=2
,所以AC=2 ,即周长为6
,即周长为6 .当x=1时,截面的周长最小,如图,
.当x=1时,截面的周长最小,如图,

设△EFG的边长为 ,BF2+BE2=EF2=
,BF2+BE2=EF2= ,又BF=BE,所以BE=
,又BF=BE,所以BE= ,连接EP交FG于点M,连接BM,因为P是等边三角形EFG的中心,所以FM=
,连接EP交FG于点M,连接BM,因为P是等边三角形EFG的中心,所以FM= ,所以EM2=EF2-FM2=
,所以EM2=EF2-FM2= 2,因为EP=
2,因为EP= EM,所以EP=
EM,所以EP=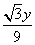 .又BP2+EP2=BE2,即12+
.又BP2+EP2=BE2,即12+ ,得y=3
,得y=3 ,所以值域为[3
,所以值域为[3 ,6
,6 ](或由平面AB1C∥平面FEG,BP=1可知E,F,G分别是BB1,AB,BC的中点,则△EFG的周长为△AB1C的一半,即3
](或由平面AB1C∥平面FEG,BP=1可知E,F,G分别是BB1,AB,BC的中点,则△EFG的周长为△AB1C的一半,即3 ).
).


科目:高中数学 来源: 题型:
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
A.DC1⊥D1P
B.平面D1A1P⊥平面A1AP
C.∠APD1的最大值为90°
D.AP+PD1的最小值为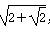
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=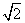 ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
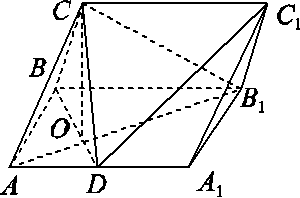
(1)证明:BC⊥AB1;
(2)若OC=OA,求三棱锥C1-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x),g(x)分别为R上的奇函数和偶函数,且满足f(x)-g(x)=ex,则有( )
A.f(2)<f(3)<g(0) B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3) D.g(0)<f(2)<f(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com