
【题目】已知函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() ,对于命题“若
,对于命题“若![]() ,则
,则![]() ”,有下列结论:
”,有下列结论:
①此命题的逆命题为真命题;
②此命题的否命题为真命题;
③此命题的逆否命题为真命题;
④此命题的逆命题和否命题有且只有一个为真命题.
其中正确的结论的序号为______________.
科目:高中数学 来源: 题型:
【题目】张三同学从每年生日时对自己的身高测量后记录如表:
![]()
(附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,![]() )
)
(1)求身高![]() 关于年龄
关于年龄![]() 的线性回归方程;(可能会用到的数据:
的线性回归方程;(可能会用到的数据:![]() (cm))
(cm))
(2)利用(1)中的线性回归方程,分析张三同学![]() 岁起到
岁起到![]() 岁身高的变化情况,如
岁身高的变化情况,如 ![]() 岁之前都符合这一变化,请预测张三同学
岁之前都符合这一变化,请预测张三同学 ![]() 岁时的身高。
岁时的身高。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 长轴长是2,点
长轴长是2,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴,以相同的长度单位建立极坐标系.己知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(1)设t为参数,若![]() ,求直线
,求直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(2)已知:直线![]() 与曲线C交于A,B两点,设
与曲线C交于A,B两点,设![]() ,且
,且![]() ,
,![]() ,
,![]() 依次成等比数列,求实数a的值.
依次成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体SABC中若三条侧棱SA,SB,SC两两互相垂直,且SA=1,SB=![]() ,SC=
,SC=![]() ,则四面体ABCD的外接球的表面积为( )
,则四面体ABCD的外接球的表面积为( )
A.8πB.6πC.4πD.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆C上,且
在椭圆C上,且![]() ⊥
⊥![]()
![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l与椭圆C交于A,B两点,![]() ,若直线l始终与圆
,若直线l始终与圆![]() 相切,求半径r的值.
相切,求半径r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]()
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此次博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台且全部售完,每万台的销售收入
万台且全部售完,每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)满足如下关系式:
(万台)满足如下关系式: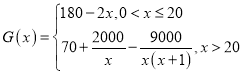 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com