Question

6．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为正方形，PD=AD=2，M，N分别为线段AC上的点．若∠MBN=30°，则三棱锥M-PNB体积的最小值为$\frac{4}{3}（2-\sqrt{3}）$．

Answer 1

分析 设∠MBH=α，∠NBH=β，根据三角函数关系得到$α+β=\frac{π}{6}$，根据三棱锥的体积公式，结合三角函数的辅助角公式进行求解即可．

解答 解：由题意值V_M-PNB=V_P-MNB=$\frac{2}{3}$S_△MNB=$\frac{2}{3}$×$\frac{1}{2}sin30°•BM•BN=\frac{1}{6}BM•BN$，
过B作BH⊥AC于H，如图：
不妨设∠MBH=α，∠NBH=β，
由BH=$\sqrt{2}$知，V_M-PNB=$\frac{1}{6}×\frac{\sqrt{2}}{cosα}•\frac{\sqrt{2}}{cosβ}$=$\frac{1}{3cosαcosβ}$，$α+β=\frac{π}{6}$，
∴V_M-PNB=$\frac{1}{6}×\frac{\sqrt{2}}{cosα}•\frac{\sqrt{2}}{cosβ}$=$\frac{1}{3cosαcosβ}$=$\frac{1}{3cosαcos（\frac{π}{6}-α）}$=$\frac{1}{3cosα（\frac{\sqrt{3}}{2}cosα+\frac{1}{2}sinα）}$
=$\frac{4}{3}•\frac{1}{\sqrt{3}+2sin（2α+\frac{π}{3}）}$$≥\frac{4}{3}•\frac{1}{2+\sqrt{3}}$=$\frac{4}{3}（2-\sqrt{3}）$，当且仅当$α=\frac{π}{12}$时，取等号．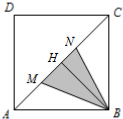
故答案为：$\frac{4}{3}（2-\sqrt{3}）$

点评 本题主要考查空间三棱锥的体积的计算，利用三角函数法，结合三角函数辅助角公式以及三角函数的有界性是解决本题的关键．综合性较强，难度较大．