Question

20．已知圆M过定点（2，0），圆心M在抛物线y²=4x上运动，若y轴截圆M所得的弦为AB，则|AB|等于（　　）

• A． 4
• B． 3
• C． 2
• D． 1

Answer 1

分析 画出图形，可根据条件设$M（\frac{{{y}_{0}}^{2}}{4}，{y}_{0}）$，并可得出圆M的半径，从而得出圆M的方程为$（x-\frac{{{y}_{0}}^{2}}{4}）^{2}+（y-{y}_{0}）^{2}=（\frac{{{y}_{0}}^{2}}{4}-2）^{2}+{{y}_{0}}^{2}$，这样令x=0便可求出y，即求出A，B点的坐标，根据A，B点的坐标便可得出|AB|．

解答 解：如图，圆心M在抛物线y²=4x上；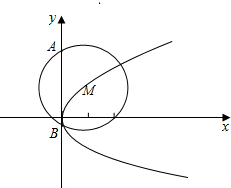

∴设$M（\frac{{{y}_{0}}^{2}}{4}，{y}_{0}）$，r=$\sqrt{（\frac{{{y}_{0}}^{2}}{4}-2）^{2}+{{y}_{0}}^{2}}$；
∴圆M的方程为：$（x-\frac{{{y}_{0}}^{2}}{4}）^{2}+（y-{y}_{0}）^{2}=（\frac{{{y}_{0}}^{2}}{4}-2）^{2}+{{y}_{0}}^{2}$；
令x=0，$\frac{{{y}_{0}}^{4}}{16}+（y-{y}_{0}）^{2}=\frac{{{y}_{0}}^{4}}{16}-{{y}_{0}}^{2}+4+{{y}_{0}}^{2}$；
∴$（y-{y}_{0}）^{2}=4$；
∴y=y₀±2；
∴|AB|=y₀+2-（y₀-2）=4．
故选：A．

点评 考查抛物线上的点和抛物线方程的关系，圆的半径和圆心，以及圆的标准方程，直线和圆的交点的求法，坐标轴上的两点的距离．