
【题目】已知![]() 为等差数列,且
为等差数列,且![]() ,其前8项和为52,
,其前8项和为52, ![]() 是各项均为正数的等比数列,且满足
是各项均为正数的等比数列,且满足![]() ,
, ![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为![]() 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留
平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留![]() 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为
米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为![]() 米,如图所示.
米,如图所示.

(1)将两个养殖池的总面积![]() 表示
表示![]() 为的函数,并写出定义域;
为的函数,并写出定义域;
(2)当温室的边长![]() 取何值时,总面积
取何值时,总面积![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值![]() (
(![]() 值越大产品的性能越好)与这种新合金材料的含量
值越大产品的性能越好)与这种新合金材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时,![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时,![]() .测得部分数据如下表:
.测得部分数据如下表:
| 0 | 2 | 6 | 10 | … |
|
| 8 | 8 |
| … |
(Ⅰ)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(Ⅱ)求该新合金材料的含量![]() 为何值时产品的性能达到最佳.
为何值时产品的性能达到最佳.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【安徽省滁州市2018届高三上学期期末考试数学】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
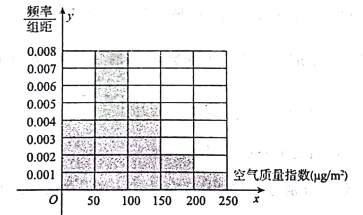
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,记这
天进行空气颗粒物分析,记这![]() 天中空气质量指数在
天中空气质量指数在![]() 的天数为
的天数为![]() ,求
,求![]() 的分布列;
的分布列;
(3)以频率估计概率,根据上述情况,若在一年![]() 天中随机抽取
天中随机抽取![]() 天,记空气质量指数在
天,记空气质量指数在![]() 以上(含
以上(含![]() )的天数为
)的天数为![]() ,求
,求![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
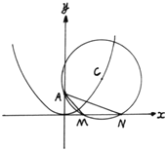
【题目】如图,已知![]() 过点
过点![]() ,圆心C在抛物线
,圆心C在抛物线![]() 上运动,若MN为
上运动,若MN为![]() 在x轴上截得的弦,设
在x轴上截得的弦,设![]() ,
,![]() ,
,![]()
![]() 当C运动时,
当C运动时,![]() 是否变化?证明你的结论.
是否变化?证明你的结论.
![]() 求
求![]() 的最大值,并求出取最大值时
的最大值,并求出取最大值时![]() 值及此时
值及此时![]() 方程.
方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为F,左顶点为A,已知
的左焦点为F,左顶点为A,已知![]() ,其中O为坐标原点,e为椭圆的离心率.
,其中O为坐标原点,e为椭圆的离心率.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 是否存在斜率为
是否存在斜率为![]() 的直线l,使得当直线l与椭圆C有两个不同交点M,N时,能在直线
的直线l,使得当直线l与椭圆C有两个不同交点M,N时,能在直线![]() 上找到一点P,在椭圆C上找到一点Q,满足
上找到一点P,在椭圆C上找到一点Q,满足![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com