
分析 (1)把a=e代入函数解析式,求出导函数的零点,可得原函数在[0,1]上单调递减,在(1,2]上单调递增,结合f(2)-f(0)>0,可得函数y=f(x)在区间x∈[0,2]上的最大值;
(2)求出原函数的导函数,分0<a<1和a>1求得原函数的最小值,由最小值等于0求得a值.
解答 解:(1)当a=e时,f(x)=ex-e(x+1)lne-$\frac{1}{e}$=ex-e(x+1)-$\frac{1}{e}$,
∴f′(x)=ex-e,
令f′(x)=0,解得x=1,
当x∈[0,1]时,f′(x)<0,函数f(x)单调递减,
当x∈(1,2]时,f′(x)>0,函数f(x)单调递增,
∵f(0)=1-e-$\frac{1}{e}$,f(2)=e2-3e-$\frac{1}{e}$,
∴f(2)-f(0)=e2-3e-$\frac{1}{e}$-1+e+$\frac{1}{e}$=e2-2e-1>0,
∴函数y=f(x)在区间x∈[0,2]上的最大值为e2-3e-$\frac{1}{e}$;
(2)f′(x)=axlna-elna=lna(ax-e),
当0<a<1时,由f′(x)=axlna-elna=lna(ax-e)<0,得ax-e>0,即x$<\frac{1}{lna}$.
由f′(x)=axlna-elna=lna(ax-e)>0,得ax-e<0,即x$>\frac{1}{lna}$.
∴f(x)在(-∞,$\frac{1}{lna}$)上为减函数,在($\frac{1}{lna}$,+∞)上为增函数,
∴当x=$\frac{1}{lna}$时函数取得最小值为f($\frac{1}{lna}$)=${a}^{\frac{1}{lna}}-e(\frac{1}{lna}+1)lna-\frac{1}{a}$=${a}^{\frac{1}{lna}}-elna-e-\frac{1}{a}$.
要使函数f(x)只有一个零点,则${a}^{\frac{1}{lna}}-elna-e-\frac{1}{a}=0$,得a=$\frac{1}{e}$;
当a>1时,由f′(x)=axlna-elna=lna(ax-e)<0,得ax-e<0,即x$<\frac{1}{lna}$.
由f′(x)=axlna-elna=lna(ax-e)>0,得ax-e>0,即x$>\frac{1}{lna}$.
∴f(x)在(-∞,$\frac{1}{lna}$)上为减函数,在($\frac{1}{lna}$,+∞)上为增函数,
∴当x=$\frac{1}{lna}$时函数取得最小值为f($\frac{1}{lna}$)=${a}^{\frac{1}{lna}}-e(\frac{1}{lna}+1)lna-\frac{1}{a}$=${a}^{\frac{1}{lna}}-elna-e-\frac{1}{a}$.
要使函数f(x)只有一个零点,则${a}^{\frac{1}{lna}}-elna-e-\frac{1}{a}=0$,得a=$\frac{1}{e}$(舍).
综上,若函数f(x)只有一个零点,则a=$\frac{1}{e}$.
点评 本题考查利用导数研究函数的单调性,考查函数零点的判定,体现了数学转化思想方法和分类讨论的数学思想方法,是压轴题.


科目:高中数学 来源: 题型:解答题
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
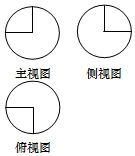 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $-\frac{7}{8}$ | C. | $-\frac{5}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com