
 ДіЦ°іЖЅъј¶ЖА¶Ё»ъ№№¶ФІОјУДіґОЧЁТµјјКхїјКФµД100ИЛµДіЙјЁЅшРРБЛНіјЖЈ¬»жЦЖБЛЖµВК·ЦІјЦ±·ЅНјЈЁИзНјЛщКѕЈ©Ј¬№ж¶Ё80·Цј°ТФЙПХЯЅъј¶іЙ№¦Ј¬·сФтЅъј¶К§°ЬЈ®
ДіЦ°іЖЅъј¶ЖА¶Ё»ъ№№¶ФІОјУДіґОЧЁТµјјКхїјКФµД100ИЛµДіЙјЁЅшРРБЛНіјЖЈ¬»жЦЖБЛЖµВК·ЦІјЦ±·ЅНјЈЁИзНјЛщКѕЈ©Ј¬№ж¶Ё80·Цј°ТФЙПХЯЅъј¶іЙ№¦Ј¬·сФтЅъј¶К§°ЬЈ®| Ѕъј¶іЙ№¦ | Ѕъј¶К§°Ь | єПјЖ | |
| ДР | 16 | ||
| Е® | 50 | ||
| єПјЖ |
| PЈЁK2ЎЭk0Ј© | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
·ЦОц ЈЁўсЈ©УЙЖµВКєНОЄ1Ј¬БРіц·ЅіМЗуaµДЦµЈ»
ЈЁўтЈ©УЙЖµВК·ЦІјЦ±·ЅНјЗуіцЅъј¶іЙ№¦µДЖµВКЈ¬јЖЛгЅъј¶іЙ№¦µДИЛКэЈ¬
МоРґБРБЄ±нЈ¬јЖЛг№ЫІвЦµЈ¬¶ФХХБЩЅзЦµµГіцЅбВЫЈ»
ЈЁўуЈ©УЙЖµВК·ЦІјЦ±·ЅНјЦЄЅъј¶К§°ЬµДЖµВКЈ¬Ѕ«ЖµВККУОЄёЕВКЈ¬
ЦЄЛж»ъ±дБїX·юґУ¶юПо·ЦІјЈ¬јЖЛг¶ФУ¦µДёЕВКЦµЈ¬Рґіц·ЦІјБРЈ¬јЖЛгКэС§ЖЪНыЈ»
Ѕвґр ЅвЈєЈЁўсЈ©УЙЖµВК·ЦІјЦ±·ЅНјёчРЎі¤·ЅРОГж»эЧЬєНОЄ1Ј¬
їЙЦЄЈЁ2a+0.020+0.030+0.040Ј©ЎБ10=1Ј¬
ЅвµГa=0.005Ј»
ЈЁўтЈ©УЙЖµВК·ЦІјЦ±·ЅНјЦЄЈ¬Ѕъј¶іЙ№¦µДЖµВКОЄ0.20+0.05=0.25Ј¬
ЛщТФЅъј¶іЙ№¦µДИЛКэОЄ100ЎБ0.25=25ЈЁИЛЈ©Ј¬
Мо±нИзПВЈє
| Ѕъј¶іЙ№¦ | Ѕъј¶К§°Ь | єПјЖ | |
| ДР | 16 | 34 | 50 |
| Е® | 9 | 41 | 50 |
| єПјЖ | 25 | 75 | 100 |
| X | 0 | 1 | 2 | 3 | 4 |
| PЈЁX=kЈ© | $\frac{1}{256}$ | $\frac{3}{64}$ | $\frac{54}{256}$ | $\frac{108}{256}$ | $\frac{81}{256}$ |
µгЖА ±ѕМвїјІйБЛЖµВК·ЦІјЦ±·ЅНјУл¶АБўРФјмСйєНАлЙўРНЛж»ъ±дБїµД·ЦІјБРЎўКэС§ЖЪНыµДУ¦УГОКМвЈ¬КЗЦРµµМвЈ®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
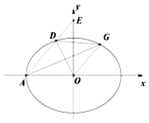 ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ТСЦЄНЦФІCЈє$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЈЁaЈѕbЈѕ0Ј©µДЧ󶥵гОЄAЈЁ-2Ј¬0Ј©Ј¬АлРДВКОЄ$\frac{\sqrt{2}}{2}$Ј¬№эAЧчР±ВКОЄkЈЁkЎЩ0Ј©µДЦ±ПЯlЅ»НЦФІCУЪµгDЈ¬Ѕ»yЦбОЄEЈ¬№эµгOЧчЦ±ПЯlµДЖЅРРПЯЅ»НЦФІУЪµгGЈ¬ЙиЎчAODЈ¬ЎчAOEЈ¬ЎчDOGµДГж»э·Ц±рОЄS1ЎўS2ЎўS3Ј®
ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ТСЦЄНЦФІCЈє$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЈЁaЈѕbЈѕ0Ј©µДЧ󶥵гОЄAЈЁ-2Ј¬0Ј©Ј¬АлРДВКОЄ$\frac{\sqrt{2}}{2}$Ј¬№эAЧчР±ВКОЄkЈЁkЎЩ0Ј©µДЦ±ПЯlЅ»НЦФІCУЪµгDЈ¬Ѕ»yЦбОЄEЈ¬№эµгOЧчЦ±ПЯlµДЖЅРРПЯЅ»НЦФІУЪµгGЈ¬ЙиЎчAODЈ¬ЎчAOEЈ¬ЎчDOGµДГж»э·Ц±рОЄS1ЎўS2ЎўS3Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
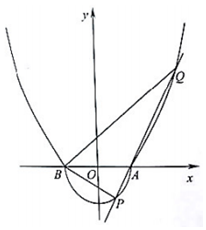 ИзНјЈ¬УЙ°лФІx2+y2=r2ЈЁyЎЬ0Ј¬rЈѕ0Ј©єНІї·ЦЕЧОпПЯy=aЈЁx2-1Ј©ЈЁyЎЭ0Ј¬aЈѕ0Ј©єПіЙµДЗъПЯCіЖОЄЎ°УрГ«ЗтРОПЯЎ±Ј¬ЗъПЯCУлxЦбУРAЎўBБЅёцЅ№µгЈ¬ЗТѕ№эµгЈЁ2.3Ј©Ј®
ИзНјЈ¬УЙ°лФІx2+y2=r2ЈЁyЎЬ0Ј¬rЈѕ0Ј©єНІї·ЦЕЧОпПЯy=aЈЁx2-1Ј©ЈЁyЎЭ0Ј¬aЈѕ0Ј©єПіЙµДЗъПЯCіЖОЄЎ°УрГ«ЗтРОПЯЎ±Ј¬ЗъПЯCУлxЦбУРAЎўBБЅёцЅ№µгЈ¬ЗТѕ№эµгЈЁ2.3Ј©Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | $\frac{1}{2}$ | BЈ® | $\frac{5}{4}$ | CЈ® | 2 | DЈ® | $\frac{3}{4}$ |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com