
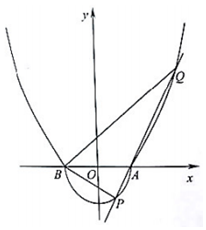
 如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).
如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).分析 (1)由将点代入抛物线方程,即可求得a的值,求得A,B点坐标,代入圆方程,即可r的值;
(2)根据两点之间的距离公式,采用分类讨论,根据二次函数的性质,即可求得|MN|的最小值;
(3)将直线方程,代入抛物线及圆的方程求得Q及P点坐标,由kBP=-kBQ,即可求得k的值,因此存在实根k=1+$\sqrt{2}$,使得∠QBA=∠PBA.
解答 解:(1)将(2,3)代入y=a(x2-1),解得:a=1,由y=x2-1与x轴交于(±1,0),
则A(1,0),B(-1,0),
代入圆x2+y2=r2,解得:r=±1,由r>0,则r=1,
∴a的值为1,r的值为1;
(2)设M(x0,y0),则丨MN丨2=x02+(y0-2)2,
当y0≤0,x02=1-y02,丨MN丨2=5-4y0,
∴当y0=0时,丨MN丨min=$\sqrt{5}$,
当y≥0时,x02=1+y0,丨MN丨2=x02+(y0-2)2=1+y0+(y0-2)2=y02-3y0+5=(y0-$\frac{3}{2}$)2+$\frac{11}{4}$,
当y0=$\frac{3}{2}$时,丨MN丨min=$\frac{\sqrt{11}}{2}$;
(3)由题意可知:PQ的方程y=k(x-1),$\left\{\begin{array}{l}{y=k(x-1)}\\{y={x}^{2}-1}\end{array}\right.$,整理得:x2-kx+k-1=0,
则x=1,y=k-1,则Q(k-1,k2-2k),
则$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,整理得:(1+k2)x2-2k2x+k2-1=0,
解得:x=1或x=$\frac{{k}^{2}-1}{{k}^{2}+1}$,
则P点坐标为($\frac{{k}^{2}-1}{{k}^{2}+1}$,-$\frac{2k}{{k}^{2}+1}$),
由∠QBA=∠PBA,
则kBP=-kBQ,即$\frac{-\frac{2k}{{k}^{2}+1}}{\frac{{k}^{2}-1}{{k}^{2}+1}+1}$=-$\frac{{k}^{2}-2k}{k}$,
即k2-2k-1=0,解得:k=1±$\sqrt{2}$(负值舍去),
因此存在实根k=1+$\sqrt{2}$,使得∠QBA=∠PBA.
点评 本题考查抛物线的性质,直线与抛物线及圆的位置关系,考查考查直线斜率的计算,考查学生的计算能力,属于中档题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
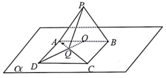 如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )| A. | $\sqrt{-3+\frac{3\sqrt{7}}{2}}$ | B. | $\sqrt{3+\frac{3\sqrt{7}}{2}}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32,$-\frac{{\sqrt{2}}}{6}-\frac{1}{3}$ | B. | 32,$\frac{{\sqrt{2}}}{6}+\frac{1}{3}$ | C. | 8,$-\frac{{\sqrt{2}}}{2}-1$ | D. | 32,$\frac{{\sqrt{2}}}{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4n | B. | 4n+1 | C. | 4n+2 | D. | 4n+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com