
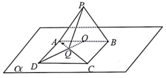
 如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )| A. | $\sqrt{-3+\frac{3\sqrt{7}}{2}}$ | B. | $\sqrt{3+\frac{3\sqrt{7}}{2}}$ | C. | $\sqrt{7}$ | D. | 3 |
分析 由题意画出图形,建立空间直角坐标系,设AB=2,∠OAD=θ(0<θ<π),把异面直线所成角的余弦值化为含有θ的三角函数式,换元后利用导数求最值.
解答 解:如图,不妨以CD在AB前侧为例.
以O为原点,分别以OB、OP所在直线为y、z轴建立空间直角坐标系,
设AB=2,∠OAD=θ(0<θ<π),则P(0,0,$\sqrt{3}$),
D(2sinθ,-1+2cosθ,0),
∴Q($\frac{2}{3}sinθ$,$\frac{2}{3}cosθ-\frac{1}{3}$,0),
∴$\overrightarrow{QP}=(-\frac{2}{3}sinθ,\frac{1}{3}-\frac{2}{3}cosθ,\sqrt{3})$,
设α与AB垂直的向量$\overrightarrow{n}=(1,0,0)$,则PQ与l所成角为α.
则|cosα|=|$\frac{\overrightarrow{QP}•\overrightarrow{n}}{|\overrightarrow{OP}||\overrightarrow{n}|}$|=|$\frac{-\frac{2}{3}sinθ}{\sqrt{\frac{32}{9}-\frac{4}{9}cosθ}}$|=$\frac{sinθ}{\sqrt{8-cosθ}}$=$\sqrt{\frac{1-co{s}^{2}θ}{8-cosθ}}$.
令t=cosθ(-1<t<1),则s=$\frac{1-{t}^{2}}{8-t}$,s′=$\frac{{t}^{2}-16t+1}{(8-t)^{2}}$,
令s′=0,得t=8-$3\sqrt{7}$,
∴当t=8-$3\sqrt{7}$时,s有最大值为16-6$\sqrt{7}$.
则cosα有最大值为$\sqrt{16-6\sqrt{7}}$,此时sinα最小值最小为$\sqrt{6\sqrt{7}-15}$.
∴正切值的最小值为$\sqrt{\frac{6\sqrt{7}-15}{16-6\sqrt{7}}}$=$\sqrt{3+\frac{3\sqrt{7}}{2}}$.
故选:B.
点评 本题考查异面直线所成角,考查空间想象能力和思维能力,训练了利用空间向量及导数求最值,属难题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
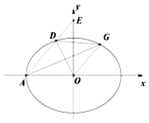 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
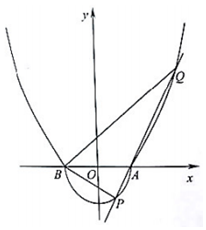 如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).
如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com