
分析 画出图形,判断直线与曲线有两个交点的范围即可.
解答 解:过定点(-2,0)的直线l与曲线C:(x-2)2+y2=4(0≤x≤3)交于不同的两点,如图: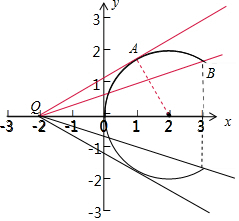
可得:k∈[kBQ,kAQ).
B(3,$\sqrt{3}$),kBQ=$\frac{\sqrt{3}-0}{3+2}$=$\frac{\sqrt{3}}{5}$,
|AQ|=$\sqrt{16-4}$=2$\sqrt{3}$,kAQ=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
由对称性可知:直线的斜率的范围:$({-\frac{{\sqrt{3}}}{3},-\frac{{\sqrt{3}}}{5}}]∪[{\frac{{\sqrt{3}}}{5},\frac{{\sqrt{3}}}{3}})$.
故答案为:$({-\frac{{\sqrt{3}}}{3},-\frac{{\sqrt{3}}}{5}}]∪[{\frac{{\sqrt{3}}}{5},\frac{{\sqrt{3}}}{3}})$.
点评 本题考查直线与曲线交点问题,考查数形结合以及转化思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{3}{2})$ | B. | $(-∞,\frac{3}{2}]$ | C. | $(-∞,\frac{9}{4})$ | D. | $(-∞,\frac{9}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
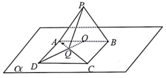 如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )
如图,平面PAB⊥平面α,AB?α,且△PAB为正三角形,点D是平面α内的动点,ABCD是菱形,点O为AB中点,AC与OD交于点Q,I?α,且l⊥AB,则PQ与I所成角的正切值的最小值为( )| A. | $\sqrt{-3+\frac{3\sqrt{7}}{2}}$ | B. | $\sqrt{3+\frac{3\sqrt{7}}{2}}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
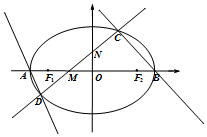 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com