
分析 (Ⅰ)由函数f(x)图象上的一个最高点为$(\frac{2}{3}π,2)$可得:M,由函数图象与y轴交点为(0,1),得$φ=\frac{π}{6}$,点$(\frac{2}{3}π,2)$在函数f(x)图象上,得$ω=3k+\frac{1}{2}$,k∈Z,即可求得ω;
(Ⅱ)由(2a-c)cosB=bcosC,得$cosB=\frac{1}{2}$,$B=\frac{π}{3}$,由(Ⅰ)得$f(A)=2sin(\frac{1}{2}A+\frac{π}{6})$,$A∈(0,\frac{2}{3}π)$.即可得函数f(A)的取值范围.
解答 解:(Ⅰ)由函数f(x)图象上的一个最高点为$(\frac{2}{3}π,2)$可得:M=2…(2分)
∵函数图象与y轴交点为(0,1),∴f(0)=2sin(0+φ)=1,$sinφ=\frac{1}{2}$
又∵$|φ|<\frac{π}{2}$,∴$φ=\frac{π}{6}$,…(4分)
∵点$(\frac{2}{3}π,2)$在函数f(x)图象上,∴$2sin(\frac{2}{3}πω+\frac{π}{6})=2$,$\frac{2}{3}πω+\frac{π}{6}=2kπ+\frac{π}{2},k∈Z$,
∴$ω=3k+\frac{1}{2}$,k∈Z,∵0<ω<3,∴$ω=\frac{1}{2}$…(6分)
(Ⅱ)由(2a-c)cosB=bcosC,得2sinAcosB-sinCcosB=sinBcosC
即2sinAcosB=sin(B+C)=sinA,∵0<A<π,∴sinA≠0,$cosB=\frac{1}{2}$,$B=\frac{π}{3}$.…(8分)
由(Ⅰ)得:$f(x)=2sin(\frac{1}{2}x+\frac{π}{6})$∴$f(A)=2sin(\frac{1}{2}A+\frac{π}{6})$
∵A+B+C=π∴$A∈(0,\frac{2}{3}π)$…(10分).
∴$\frac{A}{2}+\frac{π}{6}∈(\frac{π}{6},\frac{π}{2})$,∴$sin(\frac{A}{2}+\frac{π}{6})∈(\frac{1}{2},1)$.
∴函数f(A)的取值范围为(1,2)…(12分)
点评 本题考查了三角函数的图象,三角恒等变形,三角函数的值域,属于中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:填空题
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
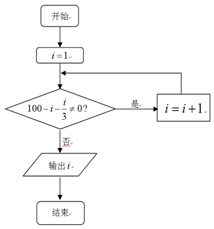 《孙子算经》中有道算术题:“今有百鹿人城,家取一鹿不尽,又三
《孙子算经》中有道算术题:“今有百鹿人城,家取一鹿不尽,又三| A. | 74 | B. | 75 | C. | 76 | D. | 77 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | 20 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com