
分析 (1)直线l的参数方程消去参数t,能求出直线l的普通方程;曲线C的极坐标方程转化为ρ2sin2θ=8ρcosθ,由此能求出曲线C的直角坐标方程.
(2)抛物线y2=8x的焦点是F(2,0),且直线l过抛物线的焦点F,由$\left\{\begin{array}{l}{y=3x-6}\\{{y}^{2}=8x}\end{array}\right.$,得9x2-44x+36=0,利用韦达定理和焦点弦公式能求出直线l被曲线C截得的弦长.
解答 解:(1)∵直线l的参数方程为$\left\{\begin{array}{l}x=4+t\\ y=3t+6\end{array}\right.$(t为参数),
∴消去参数t得直线l的普通方程为y=3x-6,
∵曲线C的极坐标方程为$ρtanθ=\frac{8}{sinθ}$,
∴ρtanθsinθ=8,即ρsin2θ=8cosθ,
∴ρ2sin2θ=8ρcosθ,
∴曲线C的直角坐标方程为y2=8x.
(2)∵抛物线y2=8x的焦点是F(2,0),且直线l过抛物线的焦点F,
设直线l与曲线C交于点A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=3x-6}\\{{y}^{2}=8x}\end{array}\right.$,得9x2-44x+36=0,
∴${x}_{1}+{x}_{2}=\frac{44}{9}$,
∴|AB|=${x}_{1}+{x}_{2}+p=\frac{44}{9}+4=\frac{80}{9}$,
∴直线l被曲线C截得的弦长为$\frac{80}{9}$.
点评 本题考查直线的普通方曲线的直角坐标方程的求法,考查线段长的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
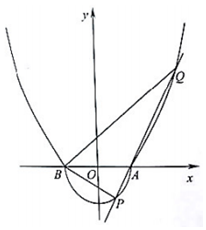 如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).
如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}-1$ | B. | $\sqrt{2}+1$ | C. | $2+\sqrt{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
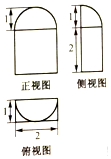
| A. | 2+π | B. | $3+\frac{π}{2}$ | C. | 3+π | D. | $4+\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com