
已知 是定义在
是定义在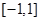 上的奇函数,且
上的奇函数,且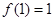 ,若
,若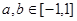 ,
,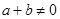 有
有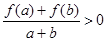 恒成立.
恒成立.
(1)判断 在
在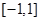 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若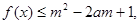 对所有
对所有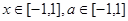 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)增函数,证明详见解析;(2)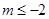 或
或 或
或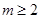
解析试题分析:(1)要判断函数的单调性一般可用增函数和减函数的定义或利用导函数判断,由于本题没有函数解析式,再结合题目特点,适于用定义判断,解决问题的关键是对照增函数和减函数的定义,再结合奇函数的条件,怎样通过适当的赋值构造出与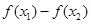 和
和 相关的式子,再判断符号解决,通过观察,只要令
相关的式子,再判断符号解决,通过观察,只要令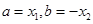 即可;(2)不等式恒成立问题一般要转化为函数的最值问题,先将原问题转化为
即可;(2)不等式恒成立问题一般要转化为函数的最值问题,先将原问题转化为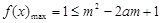 对任意
对任意 成立,再构造函数
成立,再构造函数 ,问题又转化为任意
,问题又转化为任意 恒成立,此时可对
恒成立,此时可对 的系数
的系数 的符号讨论,但较为繁琐,较为简单的做法是只要
的符号讨论,但较为繁琐,较为简单的做法是只要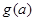 满足
满足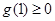 且
且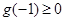 即可.
即可.
试题解析:(1)设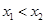 且
且 ,则
,则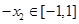 ,
, 是奇函数
是奇函数 由题设知
由题设知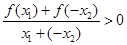 且
且 时
时 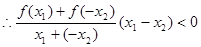 ,
,
即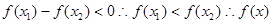 在
在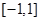 上是增函数
上是增函数
(2)由(1)知, 在
在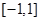 上是增函数,且
上是增函数,且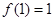

要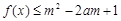 ,对所有
,对所有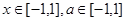 恒成立,需且只需
恒成立,需且只需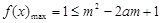 即
即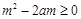 成立,
成立,
令 ,对任意
,对任意 恒成立 需且只需
恒成立 需且只需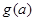 满足
满足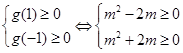 ,
,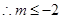 或
或 或
或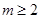
考点:函数的单调性、不等式恒成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数 在
在 处取得极值
处取得极值 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设 是曲线
是曲线 上除原点
上除原点 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于 轴的直线交曲线于点
轴的直线交曲线于点 ,试问:是否存在这样的点
,试问:是否存在这样的点 ,使得曲线在点
,使得曲线在点 处的切线与
处的切线与 平行?若存在,求出点
平行?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义域为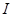 的函数
的函数 ,如果存在区间
,如果存在区间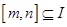 ,同时满足:
,同时满足:
① 在
在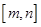 内是单调函数;②当定义域是
内是单调函数;②当定义域是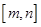 ,
, 值域也是
值域也是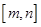 ,则称
,则称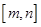 是函数
是函数
的“好区间”.
(1)设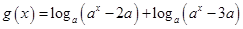 (其中
(其中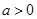 且
且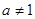 ),判断
),判断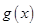 是否存在“好区间”,并
是否存在“好区间”,并
说明理由;
(2)已知函数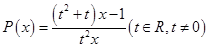 有“好区间”
有“好区间”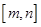 ,当
,当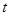 变化时,求
变化时,求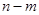 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com