
分析 (1)m=1时,化简函数f(x)=ex-lnx-2,求出函数的导数,判断函数的单调性,通过f′($\frac{1}{2}$)<0,f′(1)>0,利用零点判定定理证明即可.
(2)求出f′(x)=memx-$\frac{1}{x}$=m(emx-$\frac{1}{mx}$),利用由0<m<1得f′(x)在(0,+∞)上单调递增,由(1)得mx0=t时,f′(x0)=0,求出函数单调性以及最值,然后证明即可.
解答 证明:(1)m=1时,f(x)=ex-lnx-2,f′(x)=ex-$\frac{1}{x}$,x>0.
显然f′(x)在(0,+∞)上单调递增,又f′($\frac{1}{2}$)<0,f′(1)>0,
故存在唯一实数t∈($\frac{1}{2}$,1),使得f′(t)=0.…(4分)
(2)f′(x)=memx-$\frac{1}{x}$=m(emx-$\frac{1}{mx}$),
由0<m<1得f′(x)在(0,+∞)上单调递增,
由(1).得mx0=t时,f′(x0)=0,
所以f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
即f(x)的最小值为f(x0)=f($\frac{t}{m}$)=et-lnt+lnm-2,
∵et-$\frac{1}{t}$=0,∴et=$\frac{1}{t}$,t=-lnt.
于是f(x0)=f($\frac{t}{m}$)=$\frac{1}{t}$+t+lnm-2,所以当lnm>2-($\frac{1}{t}$+t)时,f(x)>0.
取k=2-($\frac{1}{t}$+t)<0,故m∈(ek,1)时成立.…(12分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
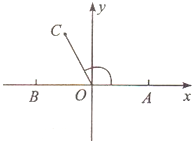 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.
如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
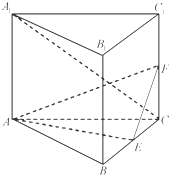 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数 ,函数
,函数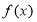 与
与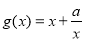 有相同极值点.
有相同极值点.
(1)求函数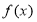 的最大值;
的最大值;
(2)求实数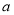 的值;
的值;
(3)若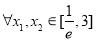 ,不等式
,不等式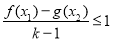 恒成立,求实数
恒成立,求实数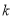 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(理)试卷(解析版) 题型:选择题
已知条件 ,条件
,条件 ,则
,则 是
是 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com