
分析 由椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1焦点在x轴,求得左焦点为F(-2$\sqrt{3}$,0),设A(x1,y1)、B(x2,y2)、C(x3,y3).根据,利用向量的坐标运算得到x1+x2+x3=-9.则$\overrightarrow{FA}$=a+ex1=4+$\frac{\sqrt{3}}{2}$x1,$\overrightarrow{FB}$=4+$\frac{\sqrt{3}}{2}$x2,$\overrightarrow{FC}$=4+$\frac{\sqrt{3}}{2}$x3,由e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,由椭圆的第二定义算出$\overrightarrow{FA}$=a+ex1=4+$\frac{\sqrt{3}}{2}$x1,同理得到$\overrightarrow{FB}$=4+$\frac{\sqrt{3}}{2}$x2,$\overrightarrow{FC}$=4+$\frac{\sqrt{3}}{2}$x3,相加并代入前面证出的等式,即可算出|$\overrightarrow{FA}$|+|$\overrightarrow{FB}$|+|$\overrightarrow{FC}$|的值.
解答 解:∵椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1焦点在x轴上,a=4,b=2,c=$\sqrt{16-4}$=2$\sqrt{3}$,
∴椭圆的左焦点为F(-2$\sqrt{3}$,0),
设A(x1,y1),B(x2,y2),C(x3,y3),
∴$\overrightarrow{FA}$=(x1+2$\sqrt{3}$,y1),$\overrightarrow{FB}$=(x2+2$\sqrt{3}$,y2),$\overrightarrow{FC}$=(x3+2$\sqrt{3}$,y3),
∵$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴(x1+2$\sqrt{3}$)+(x2+2$\sqrt{3}$)+(x3+2$\sqrt{3}$)=0,可得x1+x2+x3=-6$\sqrt{3}$.
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,由椭圆的第二定义,
得:$\overrightarrow{FA}$=a+ex1=4+$\frac{\sqrt{3}}{2}$x1,同理得到$\overrightarrow{FB}$=4+$\frac{\sqrt{3}}{2}$x2,$\overrightarrow{FC}$=4+$\frac{\sqrt{3}}{2}$x3,
∴|$\overrightarrow{FA}$|+|$\overrightarrow{FB}$|+|$\overrightarrow{FC}$|=12+$\frac{\sqrt{3}}{2}$(x1+x2+x3)=12+$\frac{\sqrt{3}}{2}$(-6$\sqrt{3}$)=3.
故答案为:3.
点评 本题考查椭圆的标准方程,考查了向量的坐标运算、椭圆的第二定义与简单几何性质等知识,考查计算能力,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [0,2] | C. | [-2,2] | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
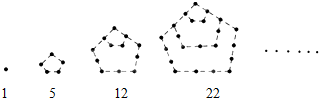 如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.
如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.01 | C. | 0.9 | D. | 0.99 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
已知函数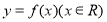 的图象过点
的图象过点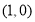 ,
,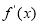 为函数
为函数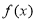 的导函数,
的导函数,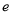 为自然对数的底数,若
为自然对数的底数,若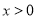 时,
时,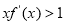 恒成立,则不等式
恒成立,则不等式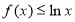 的解集为( )
的解集为( )
A.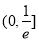 B.
B.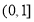
C.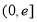 D.
D.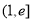
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com