
分析 (1)利用三角恒等变换化简函数的解析式,利用求得正弦函数的定义域和值域函数f(x)的值域.
(2)利用正弦函数的单调性,正弦函数的图象的对称性,求得函数f(x)的单调递增区间和其图象的对称中心.
解答 解:(1)$f(x)=\frac{1}{2}sin2x-\frac{{\sqrt{3}}}{2}cos2x=sin(2x-\frac{π}{3})$,∵x∈[${\frac{π}{12}$,$\frac{7π}{12}}$],∴2x-$\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],∴$f(x)∈[{-\frac{1}{2},1}]$.
(2)由题知,使f(x)单调递增,
则须$2x-\frac{π}{3}∈[{-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ}],k∈Z,解得x∈[{-\frac{π}{12}+kπ,\frac{5π}{12}+kπ}],k∈Z$,
∴函数f(x)的单调递增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z,
令2x-$\frac{π}{3}$=kπ,求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,故函数的图象的对称中心为($\frac{kπ}{2}$+$\frac{π}{6}$,0),k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,正弦函数的单调性,正弦函数的图象的对称性,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
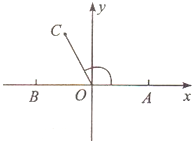 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.
如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com