
分析 (1)依题意ak=16,故数列a1,a2,…,am即为2,4,6,8,10,12,14,16,8,4共10个数,即可得出.
(2)由数列{an}满足a1=d=2,利用等差数列的通项公式可得ak=2k.而a1,am,am-1,…,ak+1,ak是首项为2、公比为2的等比数列知,${a_k}={2^{m+2-k}}$.故有2k=2m+2-k,k=2m+1-k,即k必是2的整数次幂,由k•2k=2m+1知,要使m最大,k必须最大,又k<m<2015,故k的最大值210,即可得出.
(3)由数列{an}是公差为d的等差数列知,ak=a1+(k-1)d,而a1,am,am-1,…,ak+1,ak是公比为2的等比数列${a_k}={a_1}•{2^{m+1-k}}$,a1+(k-1)d=${a_1}•{2^{m+1-k}}$,$(k-1)d={a_1}({2^{m+1-k}}-1)$,又a1+a2+…ak-1+ak=3(ak+ak+1+…+am-1+am),am=2a1,显然k≠6,则${2^{m+1-k}}=\frac{k+12}{6-k}=-1+\frac{18}{6-k}$,所以k<6,代入验证即可得出.
解答 解:(1)依题意ak=16,故数列a1,a2,…,am即为2,4,6,8,10,12,14,16,8,4共10个数,
此时m=10,Sm=84.
(2)由数列{an}满足a1=d=2,是首项为2、公差为2的等差数列知,ak=2k,
而a1,am,am-1,…,ak+1,ak是首项为2、公比为2的等比数列知,${a_k}={2^{m+2-k}}$,
故有2k=2m+2-k,k=2m+1-k,即k必是2的整数次幂,
由k•2k=2m+1知,要使m最大,k必须最大,
又k<m<2015,故k的最大值210,
从而210•21024=2m+1,m的最大值是1033.
(3)由数列{an}是公差为d的等差数列知,ak=a1+(k-1)d,
而a1,am,am-1,…,ak+1,ak是公比为2的等比数列${a_k}={a_1}•{2^{m+1-k}}$,
故a1+(k-1)d=${a_1}•{2^{m+1-k}}$,$(k-1)d={a_1}({2^{m+1-k}}-1)$
又a1+a2+…ak-1+ak=3(ak+ak+1+…+am-1+am),am=2a1
则$k{a_1}+\frac{1}{2}k(k-1)d=3×2{a_1}×\frac{{1-{2^{m-k}}}}{1-2}$,即$k{a_1}+\frac{1}{2}k[{a_1}({2^{m+1-k}}-1)]=3×2{a_1}({2^{m-k}}-1)$,
则$\frac{1}{2}k•{2^{m+1-k}}+\frac{1}{2}k=6({2^{m-k}}-1)$,即k•2m+1-k+k=6×2m+1-k-12,
显然k≠6,则${2^{m+1-k}}=\frac{k+12}{6-k}=-1+\frac{18}{6-k}$
所以k<6,将k=1,2,3,4,5一一代入验证知,
当k=4时,上式右端为8,等式成立,此时m=6,
综上可得:当且仅当m=6时,存在k=4满足等式.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [0,2] | C. | [-2,2] | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
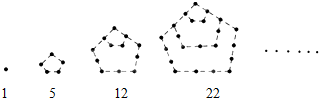 如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.
如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.01 | C. | 0.9 | D. | 0.99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com