
���� ��1������$\left\{{\begin{array}{l}{p=1}\\{q=1}\\{s=1}\end{array}}\right.$��$\left\{{\begin{array}{l}{p=1}\\{q=2}\\{s=1}\end{array}}\right.$ʱ����ӦA��ֵ���ɴ˲��룺A��B�����ҽ���p=q=sʱȡ�õȺţ�
��2���÷�����֤�����۳������ɣ�
��� �⣺��1����$\left\{{\begin{array}{l}{p=1}\\{q=1}\\{s=1}\end{array}}\right.$ʱ��A=B=1������1�֣�
��$\left\{{\begin{array}{l}{p=1}\\{q=2}\\{s=1}\end{array}}\right.$ʱ��$A=\frac{6}{5}��B=\frac{4}{3}$������3�֣�
���������p��q��s�ʣ�0��+�ޣ���
���룺A��B�����ҽ���p=q=sʱȡ�õȺţ�����6�֣�
��2��֤�����£�����p��q��s�ʣ�0��+�ޣ���
Ҫ֤$\frac{3}{{\frac{1}{p}+\frac{1}{q}+\frac{1}{s}}}��\frac{p+q+s}{3}$����������7�֣�
ֻ��֤��$9�ܣ�p+q+s����\frac{1}{p}+\frac{1}{q}+\frac{1}{s}��$��
ֻ��֤��$9��3+\frac{p}{q}+\frac{p}{s}+\frac{q}{p}+\frac{q}{s}+\frac{s}{p}+\frac{s}{q}$��
��֤��$6�ܣ�\frac{p}{q}+\frac{q}{p}��+��\frac{p}{s}+\frac{s}{p}��+��\frac{q}{s}+\frac{s}{q}��$��*��������10�֣�
�߶���p��q��s�ʣ�0��+�ޣ�����$\frac{p}{q}+\frac{q}{p}��2$��
ͬ����$\frac{p}{s}+\frac{s}{p}��2��\frac{q}{s}+\frac{s}{q}��2$��
���ʽ��*����Ȼ����������11�֣�
Ҫʹ��*���ĵȺų���������p=q=sʱ�Ⱥų�����
����ԭ����ʽ����������12�֣�
������֤������������֣�
���� ���⿼����������֤����Ӧ�����⣬Ҳ�����˹��ɲ����Ӧ�����⣬���ۺ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
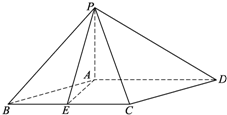 ��֪����P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���ABC=60�㣬AB=2PA��E���߶�BC���е㣮
��֪����P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���ABC=60�㣬AB=2PA��E���߶�BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k-1 | B�� | k | C�� | k+1 | D�� | k2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com