
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �� |
���� �ɼ��ϵ��Ӽ��ĸ���涨��i�����j�е���Ϊaij=$\left\{\begin{array}{l}{0{��A}_{i}��{A}_{j}=∅}\\{1��{A}_{i}��{A}_{j}��∅}\end{array}\right.$������i��j=1��2������n����ѡ��һһ�жϼ��ɣ�
��� �⣺��aij�����ע�ų�һ������Ļ������£��Խ�����ȫ��1���Խ����⣬1�ɶԳ��֣����£�
��1��a11=a22=��=ann=1��
��2����i��jʱ����aij=1����aij=1��
��aij=0����aij=0��
���Խ�����ȫ��1���Խ����⣬1�ɶԳ��֣�
���ԣ�S=n+2k��k��ijһ���Ǹ�������
����S��n����ż��һ�£���S��Сֵ��n��
����Ϊ����A1=A2=��=Anʱ��S=n2��
�ʢ٢�����ȷ�ģ�
��ѡ��B��
���� ���⿼�鼯�ϵ��Ӽ��ĸ������ĺ����������Լ��Թ涨����������ã������е��⣮


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
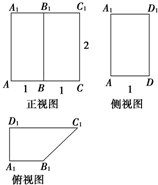
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ�ļ������У��ı���ABCDΪ�������Σ�AB��CD����DAB=60�㣬FC��ƽ��ABCD��AE��BD��CB=CD=CF��
��ͼ��ʾ�ļ������У��ı���ABCDΪ�������Σ�AB��CD����DAB=60�㣬FC��ƽ��ABCD��AE��BD��CB=CD=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-2��0] | B�� | [0��2] | C�� | [-2��2] | D�� | ��0��2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com