
分析 (1)当a=1时,化简函数求出导数,求出斜率,然后求解切线方程.
(2)求出函数f(x)的定义域是(0,+∞).通过当a>0时,求出极值点,判断函数的单调性,求出函数的最值,即可.
解答 解:(1)当a=1时,f(x)=x2-2lnx,f′(x)=2x-$\frac{2}{x}$.…(1分)
因为f′(1)=0,f(1)=1,切点为(1,1),切线斜率为0,
所以切线方程是y=1.…(4分)
(2)函数f(x)=ax2+2(a-1)x-2lnx的定义域是(0,+∞).
当a>0时,f′(x)=2ax+2(a-1)-$\frac{2}{x}$=$\frac{2a{x}^{2}+2(a-1)x-2}{x}$(x>0),
令f′(x)=0,即f′(x)=$\frac{2a{x}^{2}+2(a-1)x-2}{x}$=$\frac{2(x+1)(ax-1)}{x}$=0,
所以x=-1(舍)或x=$\frac{1}{a}$.…(8分)
当0<$\frac{1}{a}$≤1,即a≥1时,f(x)在[1,e]上单调递增,
所以f(x)在[1,e]上的最小值是f(1),由f(1)=3a-2=1,得a=1;
当1<$\frac{1}{a}$<e,即$\frac{1}{e}<a<1$时,f(x)在(1,$\frac{1}{a}$)上单调递减,在($\frac{1}{a}$,e)上单调递增,
∴f(x)在[1,e]上的最小值是f($\frac{1}{a}$),由$f(\frac{1}{a})=\frac{1}{a}+\frac{{2({a-1})}}{a}-2ln\frac{1}{a}=1$,得$ln\frac{1}{a}=\frac{a-1}{2a}$,
∵$ln\frac{1}{a}>0$,$\frac{a-1}{2a}<0$,∴当$\frac{1}{e}<a<1$时,f(x)在区间[1,e]上的最小值不为1;
当$\frac{1}{a}$≥e,即$a≤\frac{1}{e}$时,f(x)在(1,e)上单调递减,所以f(x)在[1,e]上的最小值是f(e),
由f(e)=ae2+2(a-1)e-2=1,得$a=\frac{2e+3}{{{e^2}+2e}}$,
∴$a-\frac{1}{e}=\frac{2e+3}{{{e^2}+2e}}-\frac{1}{e}=\frac{{2{e^2}+3e-{e^2}-2e}}{{e({{e^2}+2e})}}=\frac{{{e^2}+e}}{{e({{e^2}+2e})}}>0$,即$a>\frac{1}{e}$,
∴当$a≤\frac{1}{e}$时,f(x)在区间[1,e]上的最小值不为1.
综上可知,当a=1时,函数f(x)在区间[1,e]上的最小值为1.…(12分)
点评 本题考查函数的导数的应用,切线方程的求法,函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
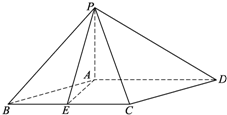 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{24π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com