练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．四棱柱ABCD-A1B1C1D1的三视图如图所示，则异面直线D1C与AC1所成的角为（　　）
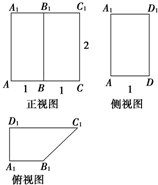
    A．30°B．45°C．60°D．90°

    分析 判断几何体是四棱柱为直四棱柱且底面为直角梯形，连结C1D，证明DC1⊥D1C，AD⊥DC1，得到DC1⊥平面ADC1，进而得到DC1⊥AC1．

    解答 解：由三视图得，该四棱柱为直四棱柱且底面为直角梯形，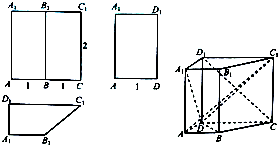

    在直四棱柱ABCD-A1B1C1D1中，连结C1D，
    ∵DC=DD1，
    ∴四边形DCC1D1是正方形，
    ∴DC1⊥D1C．
    又AD⊥CD，AD⊥DD1，DC∩DD1=D，
    ∴又AD⊥平面DCC1D1，DC1?平面DCC1D1，
    ∴AD⊥DC1
    ∵AD，DC1?平面ADC1，且AD∩DC1=D，
    ∴DC1⊥平面ADC1，
    又AC1?平面ADC1，
    ∴DC1⊥AC1；
    即异面直线D1C与AC1所成的角为90°，
    故选：D．

    点评 本题考查的知识点是棱柱的几何特征，直线与平面垂直的判定与性质，异面直线的夹角，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．设$（f（x，y））=（{\begin{array}{l}xy1\end{array}}）（{\begin{array}{l}1&0&1\\ 0&1&1\\ 1&1&{-2}\end{array}}）（{\begin{array}{l}x\\ y\\ 1\end{array}}）$，点A（x1，y1）满足方程f（x，y）=0，点B（-1，-1）．
    （1）计算$|{\overrightarrow{AB}}$|； 
    （2）O为坐标原点，当$\overrightarrow{AO}$⊥$\overrightarrow{BO}$时，计算$|{\overrightarrow{AO}}$|； 
    （3）求$|{\overrightarrow{OA}}$|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图已知椭圆C：$\frac{{x}^{2}}{4}$+y2=1，以椭圆的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0）．设圆T与椭圆C交于点M与点N．
    （1）求$\overrightarrow{TM}$•$\overrightarrow{TN}$的最小值；
    （2）设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：丨OR丨•丨OS丨为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．定义在R上的函数f（x）满足f′（x）＜1，f（1）=2，则满足f（2x-1）＜2x的x的范围是（　　）
    A．（1，+∞）B．（-∞，1）C．（-1，1）D．（-∞，1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在△ABC中，已知cosBcosC=sin2$\frac{A}{2}$，则△ABC的形状是（　　）
    A．直角三角形B．等边三角形C．等腰三角形D．等腰直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知抛物线C：x2=4y，点M（x0，y0）满足$x_0^2＜4{y_0}$，则直线l：x-x0=t（y-y0），（t∈R）与抛物线C公共点的个数是（　　）
    A．0B．1C．2D．1或2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知圆C：x2+y2=5．
    （1）求直线y=x+2被圆C截得的弦长；
    （2）求过点$N（\begin{array}{l}{1，}3\end{array}）$的圆的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

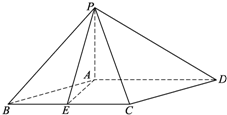    4．已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，AB=2PA，E是线段BC的中点．
    （Ⅰ）求异面直线PE和CD所成的角的余弦值；
    （Ⅱ）求平面PAE与平面PCD所成锐二面角的余弦值；
    （Ⅲ）在线段PD上是否存在一点F，使得CF∥平面PAE，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设A1，A2，A3，…，An是集合{1，2，3，…，n}的n个非空子集（n≥2），定义aij=$\left\{\begin{array}{l}{0{，A}_{i}∩{A}_{j}=∅}\\{1，{A}_{i}∩{A}_{j}≠∅}\end{array}\right.$，其中i，j=1，2，…，n，这样得到的n2个数之和记为S（A1，A2，A3，…，An），简记为S，下列三种说法：①S与n的奇偶性相同；②S是n的倍数；③S的最小值为n，最大值为n2．其中正确的判断是（　　）
    A．①②B．①③C．②③D．③

    查看答案和解析>>

    同步练习册答案