
分析 (1)利用定义,可得${({x_1}+1)^2}+{({y_1}+1)^2}={2^2}\end{array}$,所以A在以(-1,-1)为圆心,2为半径的圆上,即可计算$|{\overrightarrow{AB}}$|;
(2)O为坐标原点,当$\overrightarrow{AO}$⊥$\overrightarrow{BO}$时,利用勾股定理计算$|{\overrightarrow{AO}}$|;
(3)当$\overrightarrow{OA}$与$\overrightarrow{OB}$同向时,${\overrightarrow{OA}_{max}}=2+\sqrt{2}$,当$\overrightarrow{OA}$与$\overrightarrow{OB}$反向时,$\overrightarrow{OA}min$=2-$\sqrt{2}$,求$|{\overrightarrow{OA}}$|的取值范围.
解答 解:(1)$(f(x,y))=({\begin{array}{l}xy1\end{array}})({\begin{array}{l}1&0&1\\ 0&1&1\\ 1&1&{-2}\end{array}})({\begin{array}{l}x\\ y\\ 1\end{array}})$=(x2+y2+2x+2y-2),
∴${({x_1}+1)^2}+{({y_1}+1)^2}={2^2}\end{array}$
∴点A在以(-1,-1)为圆心,2为半径的圆上.所以$|{\overrightarrow{AB}}|=2$;$(2)∵\overrightarrow{AB}⊥\overrightarrow{BO}∴{|{\overrightarrow{AO}}|^2}={|{\overrightarrow{AB}}|^2}-{|{\overrightarrow{OB}}|^2}={2^2}-{(\sqrt{2})^2}=2∴|{\overrightarrow{AO}}|=\sqrt{2}$;
(3)当$\overrightarrow{OA}$与$\overrightarrow{OB}$同向时,${\overrightarrow{OA}_{max}}=2+\sqrt{2}$,当$\overrightarrow{OA}$与$\overrightarrow{OB}$反向时,$\overrightarrow{OA}min$=2-$\sqrt{2}$,
∴$|{\overrightarrow{AO}}|∈[{2-\sqrt{2},2+\sqrt{2}}]$.
点评 本题考查轨迹方程,考查向量知识的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
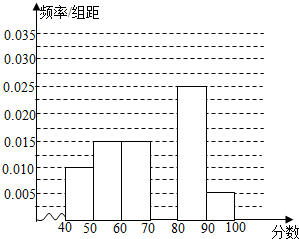 某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com