
 如图已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
如图已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.分析 (1)T(-2,0).点M与点N关于x轴对称,设M(x1,y1),N(x1,-y1),不妨设y1>0.由于点M在椭圆C上,${y}_{1}^{2}$=1-$\frac{{x}_{1}^{2}}{4}$,可得$\overrightarrow{TM}$•$\overrightarrow{TN}$=$\frac{5}{4}({x}_{1}+\frac{8}{5})^{2}$-$\frac{1}{5}$,由于-2<x1<2,可得$\overrightarrow{TM}$•$\overrightarrow{TN}$取得最小值.
(2)设P(x0,y0),则直线MP的方程为:y-y0=$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$(x-x0),令y=0,得xR=$\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{{y}_{0}-{y}_{1}}$,同理:xS=$\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{y}_{0}+{y}_{1}}$,xR•xS=$\frac{{x}_{1}^{2}{y}_{0}^{2}-{x}_{0}^{2}{y}_{1}^{2}}{{y}_{0}^{2}-{y}_{1}^{2}}$,又点M与点P在椭圆上,故${x}_{0}^{2}=4(1-{y}_{0}^{2})$,${x}_{1}^{2}$=4$(1-{y}_{1}^{2})$,代入丨OR丨•丨OS丨=|xR•xS|,化简即可证明.
解答 (1)解:依题意,得a=2,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,T(-2,0).
点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,∴${y}_{1}^{2}$=1-$\frac{{x}_{1}^{2}}{4}$,(*)
$\overrightarrow{TM}$=(x1+2,y1),$\overrightarrow{TN}$=(x1+2,-y1),
∴$\overrightarrow{TM}$•$\overrightarrow{TN}$=(x1+2)2-${y}_{1}^{2}$
=$({x}_{1}+2)^{2}-(1-\frac{{x}_{1}^{2}}{4})$=$\frac{5}{4}({x}_{1}+\frac{8}{5})^{2}$-$\frac{1}{5}$,
由于-2<x1<2,
故当${x}_{1}=-\frac{8}{5}$时,$\overrightarrow{TM}$•$\overrightarrow{TN}$取得最小值为-$\frac{1}{5}$.
(2)证明:设P(x0,y0),
则直线MP的方程为:y-y0=$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$(x-x0),
令y=0,得xR=$\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{{y}_{0}-{y}_{1}}$,
同理:xS=$\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{y}_{0}+{y}_{1}}$,
故xR•xS=$\frac{{x}_{1}^{2}{y}_{0}^{2}-{x}_{0}^{2}{y}_{1}^{2}}{{y}_{0}^{2}-{y}_{1}^{2}}$,(**)
又点M与点P在椭圆上,故${x}_{0}^{2}=4(1-{y}_{0}^{2})$,${x}_{1}^{2}$=4$(1-{y}_{1}^{2})$,
代入(**)式,得:xR•xS=$\frac{4(1-{y}_{1}^{2}){y}_{0}^{2}-4(1-{y}_{0}^{2}){y}_{1}^{2}}{{y}_{0}^{2}-{y}_{1}^{2}}$=$\frac{4({y}_{0}^{2}-{y}_{1}^{2})}{{y}_{0}^{2}-{y}_{1}^{2}}$=4.
∴丨OR丨•丨OS丨=|xR•xS|=4为定值.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、向量坐标运算性质,考查了推理能力与计算能力,属于难题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:解答题
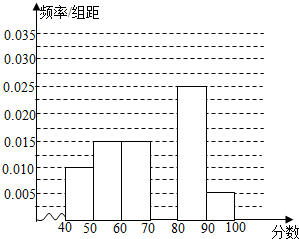 某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com