
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
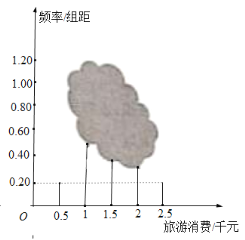
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: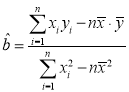 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等,更要精心设计问卷.设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况.为了调查中学生中的早恋现象,随机抽出200名学生,调查中使用了两个问题.①你的血型是A型或B型(资料:我国人口![]() 型血比例41%,
型血比例41%,![]() 型血比例28%,
型血比例28%,![]() 型血比例24%.
型血比例24%.![]() 型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
(1)试计算掷两枚骰子点数之和为偶数的机率;
(2)你能否估算出中学生早恋人数的百分比?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市工会组织了一次工人综合技能比赛,一共有![]() 名工人参加,他们的成绩都分布在
名工人参加,他们的成绩都分布在![]() 内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在
内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在![]() 分及
分及![]() 分以上的为优秀.
分以上的为优秀.

(1)求图中![]() 的值;
的值;
(2)估计这次比赛成绩的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(3)某工厂车间有![]() 名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于
名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
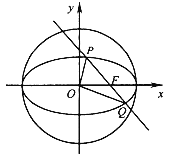
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并说明它是何种曲线;
的直角坐标方程,并说明它是何种曲线;
(2)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
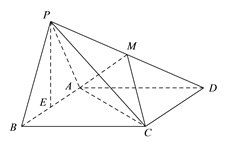
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的方程为![]() (
(![]() ),
),![]() ,
,![]() 分别为椭圆的左右焦点,A,B为椭圆E上关于原点对称两点,点M为椭圆E上异于A,B一点,直线
分别为椭圆的左右焦点,A,B为椭圆E上关于原点对称两点,点M为椭圆E上异于A,B一点,直线![]() 和直线
和直线![]() 的斜率
的斜率![]() 和
和![]() 满足:
满足:![]() .
.
(1)求椭圆E的标准方程;
(2)过![]() 作直线l交椭圆于C,D两点,且
作直线l交椭圆于C,D两点,且![]() (
(![]() ),求
),求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com