
分析 根据向量的坐标运算法则求出$\overrightarrow{a},\overrightarrow{b}$的坐标,求出数量积和模长,代入夹角公式计算.
解答 解:∵2$\overrightarrow{a}$=($\overrightarrow{a}$+$\overrightarrow{b}$)+($\overrightarrow{a}$-$\overrightarrow{b}$)=(-6,8),∴$\overrightarrow{a}$=(-3,4).
∴$\overrightarrow{b}$=$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{a}$=(5,-12).
∴$\overrightarrow{a}•\overrightarrow{b}$=-15-48=-63.|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=13.
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{63}{65}$.
点评 本题考查了平面向量的坐标运算,数量积运算,属于基础题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
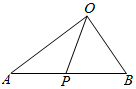 如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.
如图,在△AOB中,点P在AB上,且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$(m∈R),求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $±\frac{2\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A∪B=R | C. | A∩(∁RB)=∅ | D. | B∩(∁RA)=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | B. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | ||
| C. | $\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ | D. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com