
【题目】四位数![]() 和
和![]() 互为反序的正整数,且
互为反序的正整数,且![]() ,
,![]() 、
、![]() 分别有16个、12个正因数(包括1和本身),
分别有16个、12个正因数(包括1和本身),![]() 的质因数也是
的质因数也是![]() 的质因数,但
的质因数,但![]() 的质因数比
的质因数比![]() 的质因数少1个,求
的质因数少1个,求![]() 的所有可能值.
的所有可能值.
【答案】![]()
【解析】
设![]() ,
,![]() .则
.则![]() .
.
由![]() ,则
,则![]() .
.
故![]() ,
,![]() ,
,![]() .
.
于是,![]() ,
,![]() .
.
由![]() 为奇数,知
为奇数,知![]() 与
与![]() 一奇一偶.
一奇一偶.
若![]() 为偶数,即
为偶数,即![]() ,则
,则![]() ,
,![]() 为偶数.矛盾.
为偶数.矛盾.
因此,![]() 为偶数,
为偶数,![]() 为奇数.
为奇数.
记![]() 分解质因数后,
分解质因数后,![]() 的个数为
的个数为![]() ,2的个数为
,2的个数为![]() .则
.则![]() ,
,![]() .
.
由因数个数定理得![]() .
.
于是 ,![]() ,
,![]() .
.
所以,![]() 或8,
或8,![]() 或7.
或7.
故![]() 至多有三个质因数.
至多有三个质因数.
于是,![]() 至多含有两个质因数,3是
至多含有两个质因数,3是![]() 的一个质因数.
的一个质因数.
若![]() 只有一个质因数,则这个质因数为3.从而,
只有一个质因数,则这个质因数为3.从而,![]() ,与
,与![]() 是四位数相矛盾.
是四位数相矛盾.
因此,![]() 含有两个质因数.
含有两个质因数.
设![]() 的另一个质因数为
的另一个质因数为![]() .
.
因为![]() ,所以,
,所以,![]() 或
或![]() 或
或![]()
![]() .
.
故![]() .
.
又![]() ,则
,则![]() ,
,![]() ,即
,即![]() .
.
由![]() ,知
,知![]() .
.
此时,![]() 的值大于
的值大于![]() .
.
当![]() 时,
时,![]() .
.
而![]() 不互为反序数,于是,
不互为反序数,于是,![]() .此时,
.此时,![]() .
.
因此,![]() .于是,
.于是,![]() ,
,
![]() ,
,
![]() . ①
. ①
![]() .
.
故![]() .
.
因为![]() 为奇数,所以,
为奇数,所以,![]() 为奇数.故
为奇数.故![]() .
.
由式①得
![]() .
.
因为![]() 为偶数,所以,
为偶数,所以,![]() 为偶数.
为偶数.
于是,![]() 或8.
或8.
当![]() 时,由式①得
时,由式①得
![]() .
.
因为![]() ,所以,
,所以,![]() .
.
得![]() ,
,![]() ,
,![]() .
.
于是,![]() 或9.
或9.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
于是,![]() 或1998.
或1998.
因为![]() ,所以,
,所以,![]() .
.
又![]() ,
,![]() 符合题意.
符合题意.
因此,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:

![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
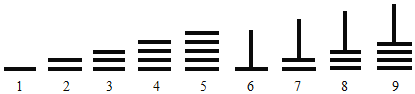
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的一个动点,点
上的一个动点,点![]()
![]() 分别在线段
分别在线段![]()
![]() 上,且满足
上,且满足![]() ,
,![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点A,B的距离之比为定值λ(λ≠1)的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系xOy中,A(-2,1),B(-2,4),点P是满足![]() 的阿氏圆上的任一点,则该阿氏圆的方程为___________________;若点Q为抛物线E:y2=4x上的动点,Q在直线x=-1上的射影为H,则
的阿氏圆上的任一点,则该阿氏圆的方程为___________________;若点Q为抛物线E:y2=4x上的动点,Q在直线x=-1上的射影为H,则![]() 的最小值为___________.
的最小值为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.
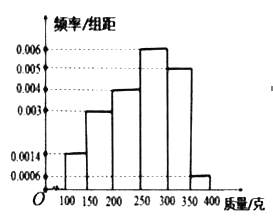
(1)估计这组数据平均数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总计,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com