
分析 由配方可得x+$\sqrt{{x^2}+{y^2}-2x+1}$=x+$\sqrt{(x-1)^{2}+{y}^{2}}$的几何意义是直线x+y=2上动点P(x,y)到A(1,0)和到y轴的距离的和,过A作直线x+y=2的对称点B,过B再作y轴的垂线,垂足为H,BH的长为最小值.计算对称点B,即可得到所求最小值.
解答 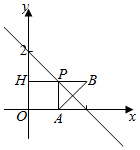 解:x+$\sqrt{{x^2}+{y^2}-2x+1}$=x+$\sqrt{(x-1)^{2}+{y}^{2}}$的几何意义是
解:x+$\sqrt{{x^2}+{y^2}-2x+1}$=x+$\sqrt{(x-1)^{2}+{y}^{2}}$的几何意义是
直线x+y=2上动点P(x,y)到A(1,0)和到y轴的距离的和,
如图,过A作直线x+y=2的对称点B,
过B再作y轴的垂线,垂足为H,BH的长为最小值.
设B(m,n),可得$\frac{n-0}{m-1}$=1,$\frac{1}{2}$(m+1)+$\frac{1}{2}$n=2,
解得m=2,n=1,
即B(2,1),则|BH|=2.
故答案为:2.
点评 本题考查最值的求法,注意运用几何意义,以及对称思想,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2)∪(2,3] | B. | [3,+∞) | C. | (1,3] | D. | (1,2)∪(2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
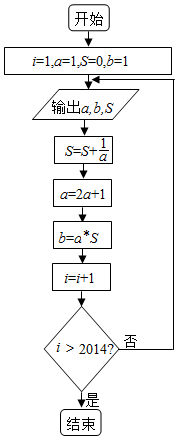 运行如图所示的程序框图,将输出的a依次记作a1,a2,…,an,输出的b依次记作b1,b2,…,bn,输出的S依次记作S1,S2,…Sn(n∈N*).
运行如图所示的程序框图,将输出的a依次记作a1,a2,…,an,输出的b依次记作b1,b2,…,bn,输出的S依次记作S1,S2,…Sn(n∈N*).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {-1,1,2} | C. | {-2,-1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com