
ЎѕМвДїЎїДіЦЦЦІОпёРИѕ![]() ІЎ¶ѕј«ТЧµјЦВЛАНцЈ¬ДіЙъОпСРѕїЛщОЄґЛНЖіцБЛТ»ЦЦї№
ІЎ¶ѕј«ТЧµјЦВЛАНцЈ¬ДіЙъОпСРѕїЛщОЄґЛНЖіцБЛТ»ЦЦї№![]() ІЎ¶ѕµДЦЖјБЈ¬ПЦ¶Ф
ІЎ¶ѕµДЦЖјБЈ¬ПЦ¶Ф![]() ЦкёРИѕБЛ
ЦкёРИѕБЛ![]() ІЎ¶ѕµДёГЦІЦкСщ±ѕЅшРРЕзОнКФСйІвКФТ©Р§.ІвКФЅб№ы·ЦЎ°ЦІЦкЛАНцЎ±єНЎ°ЦІЦкґж»оЎ±БЅёцЅб№ыЅшРРНіјЖЈ»Іў¶ФЦІЦкОьКХЦЖјБµДБї(µҐО»Јє
ІЎ¶ѕµДёГЦІЦкСщ±ѕЅшРРЕзОнКФСйІвКФТ©Р§.ІвКФЅб№ы·ЦЎ°ЦІЦкЛАНцЎ±єНЎ°ЦІЦкґж»оЎ±БЅёцЅб№ыЅшРРНіјЖЈ»Іў¶ФЦІЦкОьКХЦЖјБµДБї(µҐО»Јє![]() )ЅшРРНіјЖ№ж¶ЁЈєЦІЦкОьКХФЪ
)ЅшРРНіјЖ№ж¶ЁЈєЦІЦкОьКХФЪ![]() ЈЁ°ьАЁ
ЈЁ°ьАЁ![]() Ј©ТФЙПОЄЎ°ЧгБїЎ±Ј¬·сФтОЄЎ°І»ЧгБїЎ±.ПЦ¶ФёГ
Ј©ТФЙПОЄЎ°ЧгБїЎ±Ј¬·сФтОЄЎ°І»ЧгБїЎ±.ПЦ¶ФёГ![]() ЦкЦІЦкСщ±ѕЅшРРНіјЖЈ¬ЖдЦРЎ°ЦІЦкґж»оЎ±µД
ЦкЦІЦкСщ±ѕЅшРРНіјЖЈ¬ЖдЦРЎ°ЦІЦкґж»оЎ±µД![]() ЦкЈ¬¶ФЦЖјБОьКХБїНіјЖµГПВ±н.ТСЦЄЎ°ЦІЦкґж»оЎ±µ«Ў°ЦЖјБОьКХІ»ЧгБїЎ±µДЦІЦк№І
ЦкЈ¬¶ФЦЖјБОьКХБїНіјЖµГПВ±н.ТСЦЄЎ°ЦІЦкґж»оЎ±µ«Ў°ЦЖјБОьКХІ»ЧгБїЎ±µДЦІЦк№І![]() Цк.
Цк.
±аєЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОьКХБї |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЈЁ1Ј©НкіЙТФ![]() ПВБРБЄ±нЈ¬ІўЕР¶ПКЗ·сїЙТФФЪ·ёґнОуёЕВКІ»і¬№э
ПВБРБЄ±нЈ¬ІўЕР¶ПКЗ·сїЙТФФЪ·ёґнОуёЕВКІ»і¬№э![]() µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№ШЈї
µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№ШЈї
ОьКХЧгБї | ОьКХІ»ЧгБї | єПјЖ | |
ЦІЦкґж»о |
| ||
ЦІЦкЛАНц | |||
єПјЖ |
|
ЈЁ2Ј©ИфФЪёГСщ±ѕЎ°ЦЖјБОьКХІ»ЧгБїЎ±µДЦІЦкЦРЛж»ъійИЎ![]() ЦкЈ¬ЗуХв
ЦкЈ¬ЗуХв![]() ЦкЦРЗЎУР
ЦкЦРЗЎУР![]() ЦкЎ°ЦІЦкґж»оЎ±µДёЕВК.
ЦкЎ°ЦІЦкґж»оЎ±µДёЕВК.
ІОїјКэѕЭЈє
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Ј¬ЖдЦР
Ј¬ЖдЦР![]()
Ўѕґр°ёЎїЈЁ1Ј©Мо±нјыЅвОцЈ»І»ДЬФЪ·ёґнОуёЕВКІ»і¬№э![]() µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№ШЈЁ2Ј©
µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№ШЈЁ2Ј©![]()
ЎѕЅвОцЎї
ЈЁ1Ј©УЙМвТвМоРґБРБЄ±нЈ¬јЖЛг№ЫІвЦµЈ¬¶ФХХБЩЅзЦµµГіцЅбВЫЈ»
ЈЁ2Ј©УГБРѕЩ·ЁјЖЛг»щ±ѕКВјюКэЈ¬Зуіц¶ФУ¦µДёЕВКЦµЈ®
ЅвОцЈє(1)УЙМвТвїЙµГЎ°ЦІЦкґж»оЎ±µД![]() ЦкЈ¬Ў°ЦІЦкЛАНцЎ±µД
ЦкЈ¬Ў°ЦІЦкЛАНцЎ±µД![]() ЦкЈ»Ў°ОьКХЧгБїЎ±µД
ЦкЈ»Ў°ОьКХЧгБїЎ±µД![]() ЦкЈ¬Ў°ОьКХІ»ЧгБїЎ±µД
ЦкЈ¬Ў°ОьКХІ»ЧгБїЎ±µД![]() ЦкЈ¬МоРґБРБЄ±нИзПВЈє
ЦкЈ¬МоРґБРБЄ±нИзПВЈє
ОьКХЧгБї | ОьКХІ»ЧгБї | єПјЖ | |
ЦІЦкґж»о |
|
|
|
ЦІЦкЛАНц |
|
|
|
єПјЖ |
|
|
|
![]()
ЛщТФІ»ДЬФЪ·ёґнОуёЕВКІ»і¬№э![]() µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№Ш
µДЗ°МбПВЈ¬ИПОЄЎ°ЦІЦкµДґж»оЎ±УлЎ°ЦЖјБОьКХЧгБїЎ±УР№Ш
(2)Сщ±ѕЦРЎ°ЦЖјБОьКХІ»ЧгБїЎ±УР![]() ЦкЈ¬ЖдЦРЎ°ЦІЦкЛАНцЎ±µДУР
ЦкЈ¬ЖдЦРЎ°ЦІЦкЛАНцЎ±µДУР![]() ЦкЈ¬ґж»оµД
ЦкЈ¬ґж»оµД![]() Цк
Цк
ЙиКВјю![]() ЈєійИЎµД
ЈєійИЎµД![]() ЦкЦРЗЎУР
ЦкЦРЗЎУР![]() Цкґж»о
Цкґж»о
јЗґж»оµДЦІЦкОЄ![]() Ј¬ЛАНцµДЦІЦк·Ц±рОЄ
Ј¬ЛАНцµДЦІЦк·Ц±рОЄ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
ФтСЎИЎµД![]() ЦкУРТФПВЗйїцЈє
ЦкУРТФПВЗйїцЈє![]() Ј¬
Ј¬![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
№І![]() ЦЦЈ¬ЖдЦРЗЎУРТ»ЦкЦІЦкґж»оµДЗйїцУР
ЦЦЈ¬ЖдЦРЗЎУРТ»ЦкЦІЦкґж»оµДЗйїцУР![]() ЦЦ
ЦЦ
ЛщТФ![]() (ЖдЛы·Ѕ·ЁЧГЗйёш·Ц.)
(ЖдЛы·Ѕ·ЁЧГЗйёш·Ц.)



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() ЈЁ
ЈЁ![]() Ј©.
Ј©.
ЈЁ1Ј©ИфєЇКэ![]() УРБЅёцБгµгЈ¬ЗуКµКэaµДИЎЦµ·¶О§
УРБЅёцБгµгЈ¬ЗуКµКэaµДИЎЦµ·¶О§
ЈЁ2Ј©Ц¤ГчЈє![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() .ЈЁЖдЦРіЈКэ
.ЈЁЖдЦРіЈКэ![]() Ј¬КЗЧФИ»¶ФКэµДµЧКэЈ©
Ј¬КЗЧФИ»¶ФКэµДµЧКэЈ©
ЈЁ1Ј©Иф![]() Ј¬ЗуєЇКэ
Ј¬ЗуєЇКэ![]() µДј«ЦµµгёцКэЈ»
µДј«ЦµµгёцКэЈ»
ЈЁ2Ј©ИфєЇКэ![]() ФЪЗшјд
ФЪЗшјд![]() ЙПІ»µҐµчЈ¬Ц¤ГчЈє
ЙПІ»µҐµчЈ¬Ц¤ГчЈє![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЗъПЯ
ЦРЗъПЯ![]() µДІОКэ·ЅіМОЄ
µДІОКэ·ЅіМОЄ![]() ЈЁ
ЈЁ![]() ОЄІОКэЈ©Ј¬ТФ
ОЄІОКэЈ©Ј¬ТФ![]() ОЄј«µгЈ¬
ОЄј«µгЈ¬![]() ЦбµДХэ°лЦбОЄј«ЦбЈ¬ЅЁБўј«Чш±кПµЈ¬Ц±ПЯ
ЦбµДХэ°лЦбОЄј«ЦбЈ¬ЅЁБўј«Чш±кПµЈ¬Ц±ПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() .
.
ЈЁ1Ј©ЗуЗъПЯ![]() µДЖХНЁ·ЅіМТФј°Ц±ПЯ
µДЖХНЁ·ЅіМТФј°Ц±ПЯ![]() µДЦ±ЅЗЧш±к·ЅіМЈ»
µДЦ±ЅЗЧш±к·ЅіМЈ»
ЈЁ2Ј©Ѕ«ЗъПЯ![]() ПтЧуЖЅТЖ2ёцµҐО»Ј¬ФЩЅ«ЗъПЯ
ПтЧуЖЅТЖ2ёцµҐО»Ј¬ФЩЅ«ЗъПЯ![]() ЙПµДЛщУРµгµДєбЧш±кЛх¶МОЄФАґµД
ЙПµДЛщУРµгµДєбЧш±кЛх¶МОЄФАґµД![]() Ј¬µГµЅЗъПЯ
Ј¬µГµЅЗъПЯ![]() Ј¬ЗуЗъПЯ
Ј¬ЗуЗъПЯ![]() ЙПµДµгµЅЦ±ПЯ
ЙПµДµгµЅЦ±ПЯ![]() µДѕаАлµДЧоРЎЦµ.
µДѕаАлµДЧоРЎЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіС§РЈОЄёьєГЅшРРРЈјНЎўРЈ·з№ЬАнЈ¬ХщґґОДГчѧУЈ¬УЙЦѕФёХЯЧйіЙЎ°РЎємГ±Ў±ја¶ЅёЪЈ¬¶ФИ«РЈµДІ»ОДГчРРОЄЅшРРја¶Ѕ№ЬАнЈ¬¶ФУРІ»ОДГчРРОЄХЯЅшРРЕъЖАЅМУэЈ¬ІўЧчПкПёµДµЗјЗЈ¬ТФ±гёъЧЩµчІйПВ±нКЗ![]() ёцЦЬДЪІ»ОДГчРРОЄИЛґОНіјЖКэѕЭ:
ёцЦЬДЪІ»ОДГчРРОЄИЛґОНіјЖКэѕЭ:
ЦЬґО |
|
|
|
|
|
І»ОДГчРРОЄИЛґО |
|
|
|
|
|
ЈЁ1Ј©ЗлАыУГЛщёшКэѕЭЗуІ»ОДГчИЛґО![]() УлЦЬґО
УлЦЬґО![]() Ц®јдµД»Ш№йЦ±ПЯ·ЅіМ
Ц®јдµД»Ш№йЦ±ПЯ·ЅіМ![]() ,ІўФ¤ІвёГѧУµЪ
,ІўФ¤ІвёГѧУµЪ![]() ЦЬµДІ»ОДГчИЛґО;
ЦЬµДІ»ОДГчИЛґО;
ЈЁ2Ј©ґУµЪ![]() ЦЬµЅµЪ
ЦЬµЅµЪ![]() ЦЬјЗВјµГЦЄЈ¬ёЯТ»Дкј¶УР
ЦЬјЗВјµГЦЄЈ¬ёЯТ»Дкј¶УР![]() О»Н¬С§Ј¬ёЯ¶юДкј¶УР
О»Н¬С§Ј¬ёЯ¶юДкј¶УР![]() О»Н¬С§ТСѕУР
О»Н¬С§ТСѕУР![]() ґОІ»ОДГчРРОЄ.ѧУµВУэґ¦ѕц¶ЁПИґУХв
ґОІ»ОДГчРРОЄ.ѧУµВУэґ¦ѕц¶ЁПИґУХв![]() ИЛЦРИОСЎ
ИЛЦРИОСЎ![]() ИЛЅшРРЦШµгЅМУэ,ЗуійµЅµДБЅИЛЗЎєГАґЧФН¬Т»Дкј¶µДёЕВК
ИЛЅшРРЦШµгЅМУэ,ЗуійµЅµДБЅИЛЗЎєГАґЧФН¬Т»Дкј¶µДёЕВК
ІОїј№«КЅЈє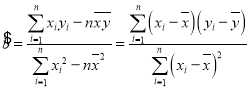 Ј¬
Ј¬![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ![]() Ј¬
Ј¬![]() КЗєЇКэ
КЗєЇКэ![]() ЈЁЖдЦРіЈКэ
ЈЁЖдЦРіЈКэ![]() Ј©НјПуЙПµДБЅёц¶ЇµгЈ¬µг
Ј©НјПуЙПµДБЅёц¶ЇµгЈ¬µг![]() Ј¬Иф
Ј¬Иф![]() µДЧоРЎЦµОЄ0Ј¬ФтєЇКэ
µДЧоРЎЦµОЄ0Ј¬ФтєЇКэ![]() µДЧоґуЦµОЄ__________Ј®
µДЧоґуЦµОЄ__________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬
Ј¬![]() .
.
ЈЁўсЈ©МЦВЫ![]() µДµҐµчРФЈ»
µДµҐµчРФЈ»
ЈЁўтЈ©µ±![]() К±Ј¬Бо
К±Ј¬Бо![]() Ј¬ЖдµјєЇКэОЄ
Ј¬ЖдµјєЇКэОЄ![]() Ј¬Йи
Ј¬Йи![]() КЗєЇКэ
КЗєЇКэ![]() µДБЅёцБгµгЈ¬ЕР¶П
µДБЅёцБгµгЈ¬ЕР¶П![]() КЗ·сОЄ
КЗ·сОЄ![]() µДБгµгЈїІўЛµГчАнУЙ.
µДБгµгЈїІўЛµГчАнУЙ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ![]() Ј¬
Ј¬![]() ЈЁ
ЈЁ![]() ЗТ
ЗТ![]() Ј©Ј¬єЇКэ
Ј©Ј¬єЇКэ![]() .
.
ЈЁ1Ј©ЗуєЇКэ![]() µДµҐµчЗшјдЈ»
µДµҐµчЗшјдЈ»
ЈЁ2Ј©ИфєЇКэ![]() µДНјПсФЪµг
µДНјПсФЪµг![]() ґ¦µДЗРПЯµДР±ВКОЄ1Ј¬ОКЈє
ґ¦µДЗРПЯµДР±ВКОЄ1Ј¬ОКЈє![]() ФЪКІГґ·¶О§ИЎЦµК±Ј¬¶ФУЪИОТвµД
ФЪКІГґ·¶О§ИЎЦµК±Ј¬¶ФУЪИОТвµД![]() Ј¬єЇКэ
Ј¬єЇКэ![]() ФЪЗшјд
ФЪЗшјд![]() ЙПЧЬґжФЪј«ЦµЈї
ЙПЧЬґжФЪј«ЦµЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛДАвЧ¶P©ЃABCDЦРЈ¬µЧГжABCDОЄЖЅРРЛД±ЯРОЈ¬ЎПDAB=45ЎгЈ¬PDЎНЖЅГжABCDЈ¬APЎНBD.
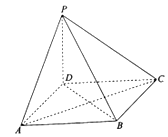
ЈЁ1Ј©Ц¤ГчЈєBCЎНЖЅГжPDBЈ¬
ЈЁ2Ј©ИфAB![]() Ј¬PBУлЖЅГжAPDЛщіЙЅЗОЄ45ЎгЈ¬ЗуµгBµЅЖЅГжAPCµДѕаАл.
Ј¬PBУлЖЅГжAPDЛщіЙЅЗОЄ45ЎгЈ¬ЗуµгBµЅЖЅГжAPCµДѕаАл.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com